Question

【题目】如图，已知中， 是边上的点，将绕点旋转，得到.

（1）当时，求证： .

（2）在（1）的条件下，猜想， ， 有怎样的数量关系，并说明理由．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】试题分析：（1）利用旋转的性质得AD=AD′，∠DAD′=∠BAC=90°，再计算出∠EAD′=∠DAE=45°，则利用“SAS”可判断△AED≌△AED′，所以DE=D′E；
（2）由（1）知△AED≌△AED′得到ED=ED′，∠B=∠ACD′，再根据等腰直角三角形的性质得∠B=∠ACB=45°，则根据性质得性质得BD=CD′，∠B=∠ACD′=45°，所以∠BCD′=∠ACB+∠ACD′=90°，于是根据勾股定理得CE2+D′C2=D′E2，所以BD2+CE==DE2．

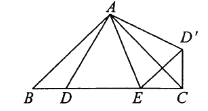
试题解析：（1）证明：∵△ABD绕点A旋转，得到△ACD′，
∴AD=AD′，∠DAD′=∠BAC=90°，
∵∠DAE=45°
∴∠EAD′=∠DAD′-∠DAE=90°-45°=45°，
∴∠EAD′=∠DAE，
在△AED与△AED′中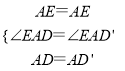
，
∴△AED≌△AED′，
∴DE=D′E；
（2）解：BD2+CE==DE2．理由如下：
由（1）知△AED≌△AED′得到：ED=ED′，∠B=∠ACD′，
在△ABC中，AB=AC，∠BAC=90°，
∴∠B=∠ACB=45°，
∵△ABD绕点A旋转，得到△ACD′
∴BD=CD′，∠B=∠ACD′=45°，
∴∠BCD′=∠ACB+∠ACD′=45°+45°=90°，
在Rt△CD′E中，CE2+D′C2=D′E2，
∴BD2+CE==DE2．