【题目】在平面直角坐标系中，直线l1：y=﹣x+4分别与x轴、y轴交于点A、点B，且与直线l2：y=x于点C．

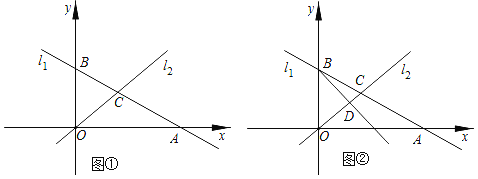
（1）如图①，求出B、C两点的坐标；

（2）若D是线段OC上的点，且△BOD的面积为4，求直线BD的函数解析式．

（3）如图②，在（2）的条件下，设P是射线BD上的点，在平面内是否存在点Q，使以O、B、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

参考答案：

【答案】（1）C（，）．（2）y=-x+4．（3）Q的坐标为（2，-2）或（-2，2）或（4，4）．

【解析】

（1）利用待定系数法求出点B坐标，利用方程组求出点C坐标即可；

（2）设D（m，m），构建方程求出m即可解决问题，再利用待定系数法求出直线的解析式；

（3）分三种情形分别求解即可解决问题；

（1）对于直线：y=- x+4，令x=0，得到y=4，

∴B（0，4），

由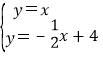，解得，

∴C（，）．

（2）∵点D在直线y=x上，设D（m，m），

∵△BOD的面积为4，

∴解得m=2，

∴D（2，2）．

设直线BD的解析式为y=kx+b，则有 ，

解得，

∴直线BD的解析式为y=-x+4．

（3）如图②中，

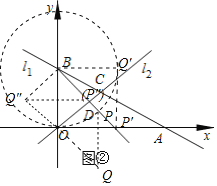
①当OB为菱形的边时，OB=PB=4，可得P（2，4-2），Q（2，-2）．

②当P′B为菱形的对角线时，四边形OBQ′P′是正方形，此时Q（4，4）．

③当OB为菱形的边时，点P″与D重合，P、Q关于y轴对称，Q″（-2，2），

综上所述，满足条件的Q的坐标为（2，-2）或（-2，2）或（4，4）．

关闭