搜索
【题目】如图，AB为半圆直径，O为圆心，C为半圆上一点，E是弧AC的中点，OE交弦AC于点D，若AC=8cm，DE=2cm，求OD的长． 
参考答案：
【答案】解：∵E为弧AC的中点，∴OE⊥AC，∴AD= 
AC=4cm， ∵OD=OE﹣DE=（OE﹣2）cm，OA=OE，
∴在Rt△OAD中，OA2=OD2+AD2即OA2=（OE﹣2）2+42 ， 又知0A=OE，解得：OE=5，
∴OD=OE﹣DE=3cm．
【解析】由E是弧AC的中点，可得：OE⊥AC．根据垂径定理得：AD= 
AC，又OD=OE﹣DE，故在Rt△OAD中，运用勾股定理可将OA的长求出．
【考点精析】关于本题考查的勾股定理的概念和垂径定理，需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，圆柱形玻璃容器高19cm，底面周长为60cm，在外侧距下底1.5cm的点A处有一只蜘蛛，在蜘蛛正对面的圆柱形容器的外侧，距上底1.5cm处的点B处有一只苍蝇，蜘蛛急于捕捉苍蝇充饥，请你帮蜘蛛计算它沿容器侧面爬行的最短距离．
-
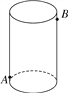
科目： 来源： 题型：
查看答案和解析>>【题目】旅客乘车按规定可以随身携带一定重量的行李，如果超过规定，则需要购买行李票，设行李费y（元）与行李重量x(千克)的关系如图，根据图象回答下列问题：
（1）行李重量在________千克以内，不必交费;
（2）当行李重量60千克时，交费____元;
（3）当行李重量________千克时，交费10元;
（4）行李重量每增加1千克，多交_________元;
（5）y= __________ ( y与x之间的关系式)
-
科目： 来源： 题型：
查看答案和解析>>【题目】谷歌人工智能AlphaGo机器人与李世石的围棋挑战赛引起人们的广泛关注，人工智能完胜李世石．某教学网站开设了有关人工智能的课程并策划了A，B两种网上学习的月收费方式：
收费
方式
月使用费(元)
包时上网
时间(h)
超时费(元/min)
A
7
25
0.6
B
10
50
0.8
设小明每月上网学习人工智能课程的时间为x小时，方案A，B的收费金额分别为yA元，yB元．
(1)当x≥50时，分别求出yA，yB与x之间的函数关系式；
(2)若小明3月份上该网站学习的时间为60小时，则他选择哪种方式上网学习合算？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC的外角∠ACD的平分线CP与∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP的度数是（ ）
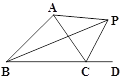
A. 30°； B. 40°； C. 50°； D. 60°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】杨辉三角是一个由数字排列成等腰三角形数表，一般形式如图所示，其中每一横行都表示
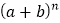（此处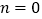
，
，
，
，
，
，
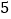）的展开式中的系数，杨辉三角最本质的特征是，它的两条斜边都是由数字组成的，而其余的数则是等于它“肩”上的两个数之和． 
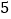
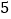
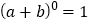
上图的构成规律你看懂了吗？
（1）请你直接写出
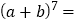__________________．杨辉三角还有另一个特征
（2）从第二行到第五行，每一行数字组成的数（如第三行为
）都是上一行的数与_____积．（3）由此你可写出
=_________________． -
科目： 来源： 题型：
查看答案和解析>>【题目】高致病性禽流感是比SARS传染速度更快的传染病．为防止禽流感蔓延，政府规定：离疫点3km范围内为扑杀区；离疫点3km～5km范围内为免疫区，对扑杀区与免疫区内的村庄、道路实行全封闭管理．现有一条笔直的公路AB通过禽流感病区，如图，在扑杀区内公路CD长为4km．
（1）请用直尺和圆规找出疫点O（不写作法，保留作图痕迹）；
（2）求这条公路在免疫区内有多少千米？
相关试题
