【题目】在平面直角坐标系xOy中,对于点P (x,y),若点Q的坐标为(ax+y,x+ay), 其中a为常数,则称点Q是点P的“a级关联点",例如,点P(1,4)的“3级关联点"为Q (3×1+4,1+3×4), 即Q (7,13)。

(1)已知点A (-2,6)的“![]() 级关联点”是点A1,点B的“2级关联点”是B1 (3, 3), 求点A1和点B的坐标:
级关联点”是点A1,点B的“2级关联点”是B1 (3, 3), 求点A1和点B的坐标:
(2)已知点M (m-1, 2m)的“-3级关联点"M位于坐标轴上,求M的坐标
参考答案:
【答案】(1)A1 (5, 1),![]() ;(2)
;(2)![]() (
(![]() ,0)或
,0)或![]() (0,-16).
(0,-16).
【解析】
(1)根据关联点的定义,结合点的坐标即可得出结论;
(2)先表示出点M(m-1,2m)的“-3级关联点”M′,然后分两种情况求解即可求出M′的坐标.
(1) ∵点A(-2, 6)的“![]() 级关联点”是点A,
级关联点”是点A,
∴A (![]() ,
,![]() ), 即A1 (5, 1).
), 即A1 (5, 1).
设点B(x, y),
∵点B的“2级关联点"是B (3, 3),
∴![]() ,
,
解得![]() ,即
,即![]() ,
,
(2) ∵点M(m-1, 2m) 的“- 3级关联点”为M (-3 (m-1) +2m, m-1+ (-3) ×2m),即![]() (-m+3, -5m-1),
(-m+3, -5m-1),
当![]() 位于x轴上,.m-1-6m= =0解得:
位于x轴上,.m-1-6m= =0解得:![]() ,
,
∴-3 (m-1) +2m=![]() ,
,
![]() ,
,
当![]() 位于y轴上,∴.-3 (m-1) +2m=0,解得: m=3,
位于y轴上,∴.-3 (m-1) +2m=0,解得: m=3,
∴![]() ,
,![]() .
.
综上所述,![]() 点坐标是
点坐标是![]() (
(![]() ,0)或
,0)或![]() (0,-16).
(0,-16).
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
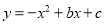 上部分点的横坐标x,纵坐标y的对应值如下表:
上部分点的横坐标x,纵坐标y的对应值如下表:x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

解答下列问题:
(1)请用含
 、
、 、
、 的代数式表示大正方形的面积.
的代数式表示大正方形的面积.方法1: ;方法2: .
(2)根据图2,利用图形的面积关系,推导
 、
、 、
、 之间满足的关系式.
之间满足的关系式.(3)利用(2)的关系式解答:如果大正方形的面积是25,且
 ,求小正方形的面积.
,求小正方形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒1cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t(t>0)秒.
(1)AC= cm;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形(直接写出结果)

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.

(1)画出△ABC关于x轴对称的图形△A1B1C1,
(2)写出点A的对应点A1的坐标;
(3)将△ABC的横、纵坐标分别乘以-1,画出对应的图形△A2B2C2;若P(a,b)为△ABC边上一点,则在△A2B2C2中,点P对应的点Q的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列的解答过程,然后再解答:
形如
 的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得
的化简,只要我们找到两个正数a、b,使a+b=m,ab=n,使得 ,
, ,那么便有:
,那么便有: (a>b)
(a>b)例如:化简

解:首先把
 化为
化为 ,这里m=7,n=12,由于4+3=7,4×3=12
,这里m=7,n=12,由于4+3=7,4×3=12即
 ,
,
∴
 =
=
(1)填空:
 = ,
= , = ;
= ;(2)化简:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】点P为等边△ABC内一点,∠APB=112°,如果把△ABP绕点A旋转,使点B与点C重合,此时点P落在点P'处,那么∠P P'C=____________度
相关试题

