【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒1cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t(t>0)秒.
(1)AC= cm;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
(3)在运动过程中,当t为何值时,△ACP为等腰三角形(直接写出结果)

参考答案:
【答案】(1)3;(2)t的值为![]() 或5s;(3)当t=
或5s;(3)当t=![]() 或3或
或3或![]() 或6s时,△ACP为等腰三角形.
或6s时,△ACP为等腰三角形.
【解析】
(1)利用勾股定理求解即可;(2)作∠ABC的平分线与AC的交点确定点P,利用全等得PC=PD,再用勾股定理求得PC的长,点P的运动路线长即可求出,由此解得t值(3)分四种情况,找到P点,即可求出t的值.
解:(1)在Rt△ABC中,∠C=90°,AB=5cm,BC=4cm,
∴AC=![]() =3cm.
=3cm.
(2)如图,过P作PD⊥AB于D,
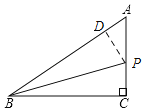
∵BP平分∠ABC,∠C=90°,
∴PD=PC,
又∵BP=BP,
∴Rt△BDP≌Rt△BCP,
∴BD=BC=4,
∴AD=5﹣4=1,
设PD=PC=y,则AP=3﹣y,
在Rt△ADP中,AD2+PD2=AP2,
∴12+y2=(3﹣y)2,
解得y=![]() ,
,
∴CP=![]() ,
,
∴t=5+4+![]() =
=![]() ;
;
当点P与点B重合时,点P也在∠ABC的角平分线上,
此时,t=5;
综上所述,点P恰好在∠ABC的角平分线上,t的值为![]() 或5s;
或5s;
(3)分四种情况:
①如图①,当AP=CP时,则∠A=∠ACP,
∵∠A+∠B=900,∠ACP+∠BCP=900,
∴∠B=∠BCP
∴BP=CP=AP
∴AP=![]()
∴ t=![]() ;
;
②如图②,当AP=AC=3时,t=3;
③当PC=AC=3时,过点C作CD⊥AB于点D,
∵S△ABC=![]() =
=![]() AB
AB![]() CD
CD
∴5CD=12,
∴CD=
∴PD=AD=![]()
∴AP=![]()
∴t=![]() ;
;
④当PC=AC=3时,BP=4-3=1,则AB+BP=5+1=6,∴t=6.
综上所述,当t=![]() 或3或
或3或![]() 或6s时,△ACP为等腰三角形.
或6s时,△ACP为等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC是等边三角形,BD是AC上的高线.作AE⊥AB于点A,交BD的延长线于点E.取BE的中点M,连结AM.

(1)求证:△AEM是等边三角形;
(2)若AE=2,求△AEM的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)课外兴趣小组活动时,老师提出了如下问题:
如图①,△ABC中,若AB=13,AC=9,求BC边上的中线AD的取值范围.
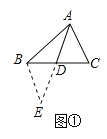
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使DE=AD,连接BE.请根据小明的方法思考:
Ⅰ.由已知和作图能得到△ADC≌△EDB,依据是 .
A.SSS B.SAS C.AAS D.HL
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是 .
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
(2)如图②,AD是△ABC的中线,BE交AC于E,交AD于F,且∠FAE=∠AFE.若AE=4,EC=3,求线段BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.
(1)如图1,求证:∠AND=∠CED;
(2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°﹣∠DBE,求证:CD=CE;
(3)如图3,在(2)的条件下,连接OF,若BE=BD+4,BC=
 ,求线段OF的长.
,求线段OF的长.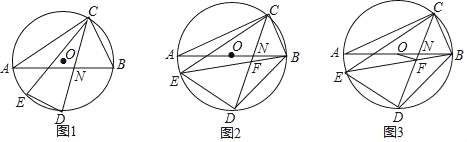
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_________处。(填数字)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于M,交AC于N.
(1)若∠ABC=70°,求∠MNA的度数.
(2)连接NB,若AB=8cm,△NBC的周长是14cm.求BC的长;

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A为某旅游景区的最佳观景点,游客可以在B处乘坐缆车沿BD方向先到达小观景平台DE观景,然后再由E处继续乘坐缆车沿EA方向到达A处,返程时从A处乘坐升降电梯直接到C处.已知AC⊥BC于C,DE∥BC,斜坡BD的坡度i=4:3,BC=210米,DE=48米,BD=100米,α=64°,则AC的高度为( )米(结果精确到0.1米,参考数据:sin64°≈0.9,tan64°≈2.1)

A. 214.2 B. 235.2 C. 294.2 D. 315.2
相关试题

