【题目】为了提高科技创新意识,我市某中学在“2016年科技节”活动中举行科技比赛,包括“航模”、“机器人”、“环保”、“建模”四个类别(每个学生只能参加一个类别的比赛),各类别参赛人数统计如图:

请根据以上信息,解答下列问题:
(1)全体参赛的学生共有 人,“建模”在扇形统计图中的圆心角是 °;
(2)将条形统计图补充完整;
(3)在比赛结果中,获得“环保”类一等奖的学生为1名男生和2名女生,获得“建模”类一等奖的学生为1名男生和1名女生,现从这两类获得一等奖的学生中各随机选取1名学生参加市级“环保建模”考察活动,问选取的两人中恰为1男生1女生的概率是多少?
参考答案:
【答案】(1)60,72;(2)详见解析;(3)![]() .
.
【解析】
试题分析:(1)由“航模”人数及其所占百分比可得总人数,用“建模”所占百分比乘以360°可得其对应圆心角度数;(2)用总人数乘以“环保”类百分比可得其人数,用总人数减去其它三个类型的人数可得“建模”人数,即可补全条形图;(3)根据题意画出树状图,然后由树状图求得所有等可能的结果与选取的两人中恰为1男生1女生的情况,再利用概率公式即可求得答案.
试题解析:(1)全体参赛的学生有:15÷25%=60(人),
“建模”在扇形统计图中的圆心角是(1﹣25%﹣30%﹣25%)×360°=72°;
(2)“环保”类人数为:60×25%=15(人),
“建模”类人数为:60﹣15﹣18﹣15=12(人),补全条形图如图:

(3)画树状图如图:

∵共有6种等可能结果,其中两人中恰为1男生1女生的有3种结果,
∴选取的两人中恰为1男生1女生的概率是:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“一个三角形中不可能有两个角是直角”用反证法证明时,首先应假设这形: _______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A. 在同圆或等圆中,同弧或等弧所对的圆周角相等
B. 平分弦的直径垂直于弦
C. 两条平行线间的距离处处相等
D. 正方形的两条对角线互相垂直平分
-
科目: 来源: 题型:
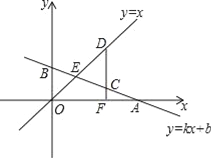
查看答案和解析>>【题目】已知函数y=kx+b的图象与x轴、y轴分别交于点A(12,0)、点B,与函数y=x的图象交于点E,点E的横坐标为3,求:
(1)直线AB的解析式;
(2)在x轴有一点F(a,0).过点F作x轴的垂线,分别交函数y=kx+b和函数y=x于点C、D,若以点B、O、C、D为顶点的四边形是平行四边形,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若∠α=54°12',则∠α的补角是_____°(结果化为度)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生的艺术特长发展情况,某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动”项目中,你最喜欢哪一项活动(每人只限一项)的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图。
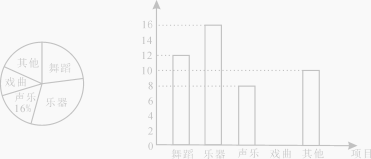
请你根据统计图解答下列问题:
(1)在这次调查中,一共抽查了 名学生。其中喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为 。扇形统计图中喜欢“戏曲”部分扇形的圆心角为 度。
(2)请你补全条形统计图。
(3)若在“舞蹈、乐器、声乐、戏曲”项目中任选两项成立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数当x=1时,y有最大值为5,且它的图象经过点(2,3),求这个函数的关系式.
相关试题

