【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 . 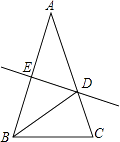
参考答案:
【答案】(1)(2)(3)
【解析】解:∵AB=AC,∠A=36°,∴∠ABC=∠C=72°,
∵DE是AB的垂直平分线,
∴AD=BD,∠ABD=∠A=36°,
∴∠DBC=72°﹣36°=36°,
∠BDC=180°﹣36°﹣72°=72°,
∴BD=BC;(1)BD平分∠ABC正确;(2)AD=BD=CD正确;(3)△BDC的周长=BC+CD+BD
=BC+CD+AD
=BC+AC
=AB+BC,正确;(4)AD=BD≠CD,所以D不是AC的中点,故本选项错误.
故正确的命题是(1)(2)(3).
【考点精析】利用线段垂直平分线的性质对题目进行判断即可得到答案,需要熟知垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
 与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
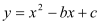 交x轴于点A(1,0),交y轴于点B,对称轴是x=2.
交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式ax3+bx+1的值为6,那么当x=-2时,这个代数式的值是( )
A. 1 B. -4 C. 6 D. -5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2008年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电.该地供电局组织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,15分钟后,电工乘吉普车从同一地点出发,结果两车同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2 .
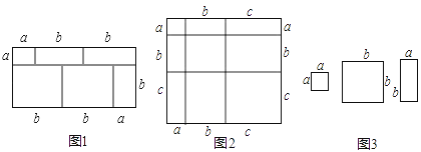
(1)由图2,可得等式:
(2)利用(1)中所得到的结论,解决下面的问题:已知 a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)小明用2 张边长为a 的正方形,3 张边长为b的正方形,5 张边长分别为a、b 的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2 .

A.72
B.90
C.108
D.144
相关试题

