【题目】如图1,抛物线![]() 与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)D(1,4),![]() ;(2)S=
;(2)S=![]() (
(![]() ),S最大值为
),S最大值为![]() ;(3)Q的坐标为(
;(3)Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).
【解析】
试题分析:(1)先把抛物线解析式变成顶点式即可得到D点坐标,再求出C点坐标,然后利用待定系数法求直线l的解析式;
(2)先求出B(3,0),再求出直线BD的解析式为![]() ,则P(x,
,则P(x,![]() ),根据梯形的面积公式可得S=
),根据梯形的面积公式可得S=![]() (
(![]() ),再利用而此函数的性质求S的最大值;
),再利用而此函数的性质求S的最大值;
(3)如图2,设Q(t,0)(t>0),则M(t,![]() ),N(t,
),N(t,![]() ),利用两点间的距离公式得到MN=
),利用两点间的距离公式得到MN=![]() ,CM=
,CM=![]() ,然后证明NM=CM得到
,然后证明NM=CM得到![]() =
=![]() ,再解方程求满足条件的t的值,从而得到点Q的坐标.
,再解方程求满足条件的t的值,从而得到点Q的坐标.
试题解析:(1)∵![]() =
=![]() ,∴D(1,4),在
,∴D(1,4),在![]() 中,当x=0时,y=3,则C(0,3),设直线l的解析式为
中,当x=0时,y=3,则C(0,3),设直线l的解析式为![]() ,把C(0,3),E(4,0)分别代入得:
,把C(0,3),E(4,0)分别代入得:![]() ,解得:
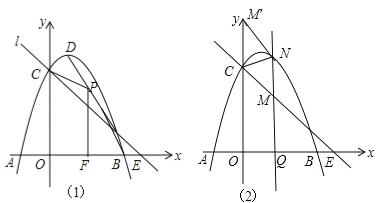
,解得: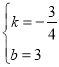 ,∴直线l的解析式为
,∴直线l的解析式为![]() ;
;
(2)如图(1),当y=0时,![]() ,解得
,解得![]() ,
,![]() ,则B(3,0),设直线BD的解析式为
,则B(3,0),设直线BD的解析式为![]() ,把B(3,0),D(1,4)分别代入得:
,把B(3,0),D(1,4)分别代入得:![]() ,解得:
,解得:![]() ,∴直线BD的解析式为
,∴直线BD的解析式为![]() ,则P(x,
,则P(x,![]() ),∴S=
),∴S=![]() =
=![]() (
(![]() ),∵S=
),∵S=![]() ,∴当x=
,∴当x=![]() 时,S有最大值,最大值为
时,S有最大值,最大值为![]() ;
;
(3)存在.
如图2,设Q(t,0)(t>0),则M(t,![]() ),N(t,
),N(t,![]() ),∴MN=
),∴MN=![]() =
=![]() ,CM=
,CM=![]() =
=![]() ,∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,而QN∥y轴,∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,∴∠M′CN=∠CNM,∴∠M′CN=∠CNM′,∴CM′=NM′,∴NM=CM,∴
,∵△CMN沿CN翻转,M的对应点为M′,M′落在y轴上,而QN∥y轴,∴MN∥CM′,NM=NM′,CM′=CM,∠CNM=∠CNM′,∴∠M′CN=∠CNM,∴∠M′CN=∠CNM′,∴CM′=NM′,∴NM=CM,∴![]() =
=![]() ,
,
当![]() =
=![]() ,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
,解得t1=0(舍去),t2=4,此时Q点坐标为(4,0);
当![]() =
=![]() ,解得t1=0(舍去),t2=
,解得t1=0(舍去),t2=![]() ,此时Q点坐标为(
,此时Q点坐标为(![]() ,0),
,0),
综上所述,点Q的坐标为(![]() ,0)或(4,0).
,0)或(4,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙、丙、丁四位同学给出了四种表示该长方形面积的多项式: ①(2a+b)(m+n); ②2a(m+n)+b(m+n);
③m(2a+b)+n(2a+b); ④2am+2an+bm+bn,你认为其中正确的有( )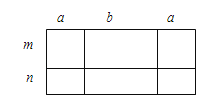
A.①②
B.③④
C.①②③
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE,设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C,F,D的抛物线为
 .
.(1)求点D的坐标(用含m的式子表示);
(2)若点G的坐标为(0,﹣3),求该抛物线的解析式;
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=
 EA?若存在,直接写出点P的坐标;若不存在,说明理由.
EA?若存在,直接写出点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.

(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2,l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
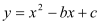 交x轴于点A(1,0),交y轴于点B,对称轴是x=2.
交x轴于点A(1,0),交y轴于点B,对称轴是x=2.(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式ax3+bx+1的值为6,那么当x=-2时,这个代数式的值是( )
A. 1 B. -4 C. 6 D. -5
-
科目: 来源: 题型:
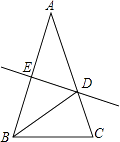
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 .
相关试题

