【题目】如图,抛物线![]() 交x轴于点A(1,0),交y轴于点B,对称轴是x=2.
交x轴于点A(1,0),交y轴于点B,对称轴是x=2.
(1)求抛物线的解析式;
(2)点P是抛物线对称轴上的一个动点,是否存在点P,使△PAB的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)存在,P(2,1).
;(2)存在,P(2,1).
【解析】
试题分析:(1)根据抛物线经过点A(1,0),对称轴是x=2列出方程组,解方程组求出b、c的值即可;
(2)因为点A与点C关于x=2对称,根据轴对称的性质,连接BC与x=2交于点P,则点P即为所求,求出直线BC与x=2的交点即可.
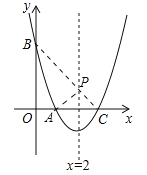
试题解析:(1)由题意得,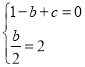 ,解得b=4,c=3,∴抛物线的解析式为.
,解得b=4,c=3,∴抛物线的解析式为.![]() ;
;
(2)∵点A与点C关于x=2对称,∴连接BC与x=2交于点P,则点P即为所求,根据抛物线的对称性可知,点C的坐标为(3,0),![]() 与y轴的交点为(0,3),∴设直线BC的解析式为:
与y轴的交点为(0,3),∴设直线BC的解析式为:![]() ,∴
,∴![]() ,解得:
,解得:![]() ,∴直线BC的解析式为:
,∴直线BC的解析式为:![]() ,则直线BC与x=2的交点坐标为:(2,1),∴点P的交点坐标为:(2,1).
,则直线BC与x=2的交点坐标为:(2,1),∴点P的交点坐标为:(2,1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),翻折矩形OABC,使点A与点C重合,得到折痕DE,设点B的对应点为F,折痕DE所在直线与y轴相交于点G,经过点C,F,D的抛物线为
 .
.(1)求点D的坐标(用含m的式子表示);
(2)若点G的坐标为(0,﹣3),求该抛物线的解析式;
(3)在(2)的条件下,设线段CD的中点为M,在线段CD上方的抛物线上是否存在点P,使PM=
 EA?若存在,直接写出点P的坐标;若不存在,说明理由.
EA?若存在,直接写出点P的坐标;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线l1;y=ax2+bx+c(a<0)经过原点,与x轴的另一个交点为B(4,0),点A为顶点,且直线OA的解析式为y=x.

(1)如图1,求抛物线l1的解析式;
(2)如图2,将抛物线l1绕原点O旋转180°,得到抛物线l2,l2与x轴交于点B′,顶点为A′,点P为抛物线l1上一动点,连接PO交l2于点Q,连接PA、PA′、QA′、QA.
请求:平行四边形PAQA′的面积S与P点横坐标x(2<x≤4)之间的关系式;
(3)在(2)的条件下,如图11﹣3,连接BA′,抛物线l1或l2上是否存在一点H,使得HB=HA′?若存在,请求出点H的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
 与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】当x=2时,代数式ax3+bx+1的值为6,那么当x=-2时,这个代数式的值是( )
A. 1 B. -4 C. 6 D. -5
-
科目: 来源: 题型:
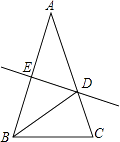
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2008年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电.该地供电局组织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,15分钟后,电工乘吉普车从同一地点出发,结果两车同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
相关试题

