【题目】如图,矩形ABCD中,AB=12cm,BC=24cm,如果将该矩形沿对角线BD折叠,那么图中阴影部分的面积( )cm2 . 
A.72
B.90
C.108
D.144
参考答案:
【答案】B
【解析】解:由折叠得到△BCD≌△BC′D,由矩形ABCD得到△ABD≌△CDB,∴△ABD≌△C′DB,
∴∠C′BD=∠ADB,
∴EB=DE,
在△ABE和△C′DE中,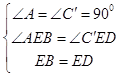 ,
,
∴△ABE≌△C′DE(AAS),
∴AE=C′E,
设AE=C′E=xcm,则有ED=AD﹣AE=(24﹣x)cm,
在Rt△ABE中,根据勾股定理得:AB2+AE2=BE2 , 即122+x2=(24﹣x)2 ,
解得:x=9,
∴AE=9cm,ED=15cm,
则S△BED= ![]() EDAB=
EDAB= ![]() ×15×12=90(cm2).
×15×12=90(cm2).
故选B
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
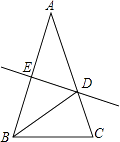
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC于D,交AB于E,下述结论:(1)BD平分∠ABC;(2)AD=BD=BC;(3)△BDC的周长等于AB+BC;(4)D是AC中点.其中正确的命题序号是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2008年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电.该地供电局组织电工进行抢修.供电局距离抢修工地15千米.抢修车装载着所需材料先从供电局出发,15分钟后,电工乘吉普车从同一地点出发,结果两车同时到达抢修工地.已知吉普车速度是抢修车速度的1.5倍,求这两种车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2 .
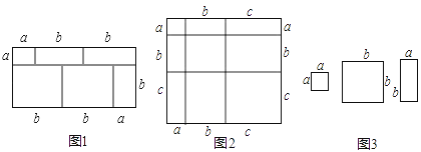
(1)由图2,可得等式:
(2)利用(1)中所得到的结论,解决下面的问题:已知 a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)利用图3中的纸片(足够多),画出一种拼图,使该拼图可用来验证等式:2a2+5ab+2b2=(2a+b)(a+2b);
(4)小明用2 张边长为a 的正方形,3 张边长为b的正方形,5 张边长分别为a、b 的长方形纸片重新拼出一个长方形,那么该长方形较长的一条边长为 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列变形正确的是( )
A.4x﹣5=3x+2变形得4x﹣3x=﹣2+5
B.﹣3x=2变形得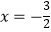
C.3(x﹣1)=2(x+3)变形得3x﹣1=2x+6
D. 变形得4x﹣6=3x+18
变形得4x﹣6=3x+18 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过坐标原点O和x轴上另一点E,顶点M的坐标为(2,4);矩形ABCD的顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3.
(1)求该抛物线所对应的函数关系式;
(2)将矩形ABCD以每秒1个单位长度的速度从如图所示的位置沿x轴的正方向匀速平行移动,同时一动点P也以相同的速度从点A出发向B匀速移动,设它们运动的时间为t秒(0≤t≤3),直线AB与该抛物线的交点为N(如图2所示).
①当t=
 时,判断点P是否在直线ME上,并说明理由;
时,判断点P是否在直线ME上,并说明理由;②设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.

-
科目: 来源: 题型:
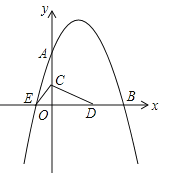
查看答案和解析>>【题目】如图,已知抛物线
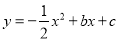 与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
相关试题

