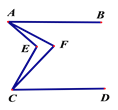
【题目】如图,已知AB‖CD,∠EAF =![]() ∠EAB,∠ECF=
∠EAB,∠ECF=![]() ∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
∠ECD ,则∠AFC与∠AEC之间的数量关系是_____________________________
参考答案:
【答案】4∠AFC=3∠AEC
【解析】分析:连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,然后根据平行线的性质得出∠AEC=4(x°+y°),∠AFC=3(x°+y°),从而得出答案.
详解:连接AC,设∠EAF=x°,∠ECF=y°,∠EAB=4x°,∠ECD=4y°,
∵AB∥CD,∴∠BAC+∠ACD=180°,∴∠CAE+4x°+∠ACE+4y°=180°,
∴∠CAE+∠ACE=180°-(4x°+4y°),∠FAC+∠FCA=180°-(3x°+3y°)
∴∠AEC=180°-(∠CAE+∠ACE)=180°-[180°-(4x°+4y°)]=4x°+4y°=4(x°+y°),
∠AFC=180°-(∠FAC+∠FCA)=180°-[180°-(3x°+3y°)]=3x°+3y°=3(x°+y°),
∴4∠AFC=3∠AEC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件B种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元。设生产A种产品的生产件数为x, A、B两种产品所获总利润为y (元)
(1)试写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.
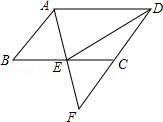
(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中:
 有公共顶点和一条公共边的两个角一定是邻补角;
有公共顶点和一条公共边的两个角一定是邻补角; 垂线段最短;
垂线段最短; 经过直线外一点,有且只有一条直线与这条直线平行;
经过直线外一点,有且只有一条直线与这条直线平行; 相等的角是对顶角;
相等的角是对顶角; 等角的余角相等,其中假命题的个数是
等角的余角相等,其中假命题的个数是
A. 0个 B. 1个 C. 2个 D. 3个
-
科目: 来源: 题型:
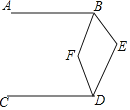
查看答案和解析>>【题目】如图,
 平分
平分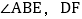 平分
平分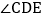 ,则
,则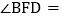 ______ .
______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB,FC.
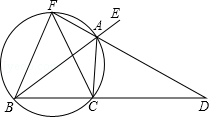
(1)求证:∠FBC=∠FCB;
(2)已知FAFD=12,若AB是△ABC外接圆的直径,FA=2,求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB和直线CD,直线BE和直线CF都被直线BC所截,在下面三个式子只,请你选择其中两个作为题设,剩下的一个作为结论,组成一个真命题并写出对应的推理过程
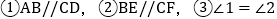 题设
题设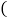 已知
已知 ;______
;______ 结论
 求证
求证 :______
:______ 理由:
相关试题

