【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
![]()
那么当n=26时,第2016次“F运算”的结果是_____.
参考答案:
【答案】62.
【解析】
根据新定义规定的运算法则分别计算出第1、2、3、…、11次的运算结果,即可发现从第11次开始,每6次运算为一个周期循环,据此可得.
根据题意,得
当n=26时,第1次的计算结果是![]() =13,
=13,
第2次的计算结果是13×3+5=44,
第3次的计算结果是![]() =11,
=11,
第4次的计算结果是11×3+5=38,
第5次的计算结果是![]() =19,
=19,
第6次的计算结果是19×3+5=62,
第7次的计算结果是![]() =31,
=31,
第8次的计算结果是31×3+5=98,
第9次的计算结果是![]() =49,
=49,
第10次的计算结果是49×3+5=152,
第11次的计算结果是![]() =19,以下每6次运算一循环,
=19,以下每6次运算一循环,
∵(20164)÷6=335…2,
∴第2016次“F运算”的结果与第6次的计算结果相同,为62,
故答案为:62.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 和矩形
和矩形 如图①摆放(点
如图①摆放(点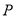 与点
与点 重合),点
重合),点 ,
,  在同一直线上,
在同一直线上,  ,
, 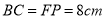 ,
,  .如图②,
.如图②, 从图①的位置出发,沿
从图①的位置出发,沿 方向匀速运动,速度为1
方向匀速运动,速度为1  ,
,  与
与 交于点
交于点 ,与BD交于点K;同时,点
,与BD交于点K;同时,点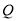 从点
从点 出发,沿
出发,沿 方向匀速运动,速度为1
方向匀速运动,速度为1  .过点
.过点 作
作 ,垂足为
,垂足为 ,交
,交 于点
于点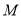 ,连接
,连接 ,当点
,当点 停止运动时,
停止运动时,  也停止运动.设运动事件为
也停止运动.设运动事件为 .解答下列问题:
.解答下列问题:(1)当为何值时,
 ?
?(2)在运动过程中,是否存在某一时刻,使
 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;(3)在运动过程中,
①当t为 秒时,以PQ为直径的圆与PE相切,
②当t为 秒时,以PQ的中点为圆心,以 cm为半径的圆与BD和BC同时相切.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ①
①  ②
② -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,
 ,
, 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点, ,垂足为G,若
,垂足为G,若 ,则AE的边长为
,则AE的边长为


A.
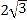 B.
B.  C. 4 D. 8
C. 4 D. 8 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠1=∠2.

(1)△ADB和△ABE相似吗?
(2)小明说:“AB2=AD·AE”,你同意吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a、b、c在数轴上对应的点如图所示,

(1)化简:2|b﹣c|﹣|b+c|+|a﹣c|﹣|a﹣b|;
(2)若(c+4)2与|a+c+10|互为相反数,且b=|a﹣c|,求(1)中式子的值.
相关试题

