【题目】已知: ![]() 和矩形
和矩形![]() 如图①摆放(点
如图①摆放(点![]() 与点
与点![]() 重合),点
重合),点![]() ,
, ![]() 在同一直线上,
在同一直线上, ![]() ,
, ![]() ,
, ![]() .如图②,
.如图②,![]() 从图①的位置出发,沿
从图①的位置出发,沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1 ![]() ,
, ![]() 与
与![]() 交于点
交于点![]() ,与BD交于点K;同时,点
,与BD交于点K;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1 ![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,当点
,当点![]() 停止运动时,
停止运动时, ![]() 也停止运动.设运动事件为
也停止运动.设运动事件为![]() .解答下列问题:
.解答下列问题:
(1)当为何值时, ![]() ?
?
(2)在运动过程中,是否存在某一时刻,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)在运动过程中,
①当t为 秒时,以PQ为直径的圆与PE相切,
②当t为 秒时,以PQ的中点为圆心,以 cm为半径的圆与BD和BC同时相切.

参考答案:
【答案】(1)![]() ;(2)t=2;(3)①t=
;(2)t=2;(3)①t=![]() ,②t=4,r=2 .
,②t=4,r=2 .
【解析】试题分析:(1)如图1中,当PQ∥BD时, ![]() ,可得
,可得![]() ,解方程即可;
,解方程即可;
(2)假设存在,如图2中,当0<t<6时,S五边形AFPQM==S△ABF+S矩形ABCD-S△CPQ-S△MDQ,由此计算出五边形AFPQM的面积.根据题意列出方程即可解决问题;
(3)①当以PQ为直径的圆与PE相切时,PQ⊥PE,可证得△PFE∽△QCP,得到![]() ,然后代入含t的式子,列出方程即可求出t的值;
,然后代入含t的式子,列出方程即可求出t的值;
②设PQ的中点为O,连接BO并延长,交CD与点J,过O作OI⊥BC,过J作JK⊥BD.由过点O的圆与BC、BD都相切可证得BJ平分∠DBC,根据角平分线的性质可得JC=JK,BK=BC=8,DK=BD-BK=2,JC=JK=x,在Rt△JKD中,由勾股定理求出JC的值,由O是PQ的中点,根据三角形中位线的性质用t表示OI,PI,进而表示出BI,然后由△BOI∽△BJC得![]() ,代入数据即可求出t的值,进而求出圆的半径.
,代入数据即可求出t的值,进而求出圆的半径.
试题解析:
解:(1)若PQ∥BD,则△CPQ∽△CBD,
∴![]() ,即
,即![]() ,
,
解得:t=![]() ;
;

(2)由∠MQD+∠CDB=∠CBD+∠CDB=90°,
可得∠MQD=∠CBD.
又∠MDQ=∠C=90°,
∴△MDQ∽△DCB,
∴![]() ,
,
即![]() ,
,
∴MD=![]() ,
,
则S五边形AFPQM==S△ABF+S矩形ABCD-S△CPQ-S△MDQ
=![]() AB×BF+AB×BC-
AB×BF+AB×BC-![]() PC×CQ-
PC×CQ-![]() MD×DQ
MD×DQ
=![]() ×6×(8-t)+6×8-
×6×(8-t)+6×8-![]() (8-t)×t-
(8-t)×t-![]() ×
×![]() ×(6-t)
×(6-t)
=![]() (0<t<6).
(0<t<6).
假使存在t,使S五边形AFPQM:S矩形ABCD=9:8,
则S五边形AFPQM=![]() S矩形ABCD=54,
S矩形ABCD=54,
即![]() =54,
=54,
整理得t2-20t+36=0,
解得t1=2,t2=18>6(舍去),
答:当t=2,S五边形AFPQM:S矩形ABCD=9:8;
(3)①当以PQ为直径的圆与PE相切时,PQ⊥PE,
∴∠EPF+∠QPC=90°,
又∵∠E+∠EPF=90°,
∴∠E=∠QPC,
∵∠EFP=∠C=90°,
∴△PFE∽△QCP,
∴![]() ,
,
∴![]() ,
,
解得t=![]() ,
,
即t=![]() 秒时,以PQ为直径的圆与PE相切;
秒时,以PQ为直径的圆与PE相切;
②设PQ的中点为O,连接BO并延长,交CD与点J,过O作OI⊥BC,过J作JK⊥BD,

∵过点O的圆与BC、BD都相切,
∴BJ平分∠DBC,
∵∠C=90°,JK⊥BD,
∴JC=JK,BK=BC=8,
DK=BD-BK=10-8=2,
设JC=JK=x,则JD=6-x,
在Rt△JKD中,由勾股定理得:x2+22=(6-x)2,
解得x=![]() ,
,
CP=BC-
∵O是PQ的中点,OI⊥BC,
∴OI=![]() CQ=
CQ=![]() t,PI=CI=
t,PI=CI=![]() (8-t)=4-
(8-t)=4-![]() t,
t,
∴BI=BP+PI=t+4-![]() t=4+
t=4+![]() t,
t,
∵OI⊥BC,∠C=90°,
∴OI∥JC,
∴△BOI∽△BJC,
∴![]() ,
,
即 ,
,
解得t=4,
此时圆的半径为OI=![]() t=2.
t=2.
故答案为:4,2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习绝对值后,我们知道,|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离.而|5|=|5﹣0|,即|5﹣0|也可理解为5、0在数轴上对应的两点之间的距离.类似的,|5-3|表示5与3之差的绝对值,也可理解为5与3两数在数轴上所对应的两点之间的距离.如|x-3|的几何意义是数轴上表示有理数3的点与表示数x的点之间的距离,一般地,点A、B在数轴上分别表示数a、b,那么A、B之间的距离可表示为|a﹣b|.
请根据绝对值的意义并结合数轴解答下列问题:
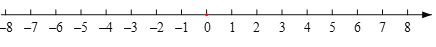
(1)数轴上表示2和3的两点之间的距离是 ;数轴上表示数a的点与表示﹣2的点之间的距离表示为 ;
(2)数轴上点P表示的数是2,P、Q两点的距离为3,则点Q表示的数是 ;
(3)数轴上有一个点表示数a,则|a+1|+|a-3|+|a+8|的最小值为 ;
(4)a、b、c、d在数轴上的位置如下图所示,若|a-d|=12,|b-d|=7,|a-c|=9,则|b-c|等于 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-23-(-58)+(-5) ;
(2)3×(2)+38;
(3) (
 +
+ -
- )×(-24)
)×(-24)(4)0.5+(15)(17)|12|
(5)
-
科目: 来源: 题型:
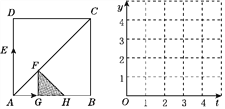
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,动点E从点A出发,以每秒2个单位的速度沿A→D→A运动,动点G从点A出发,以每秒1个单位的速度沿A→B运动,当有一个点到达终点时,另一点随之也停止运动.过点G作FG⊥AB交AC于点F.设运动时间为t(单位:秒).以FG为一直角边向右作等腰直角三角形FGH,△FGH与正方形ABCD重叠部分的面积为S.
(1)当t=1.5时,S=________;当t=3时,S=________.
(2)设DE=y1,AG=y2,在如图所示的网格坐标系中,画出y1与y2关于t的函数图象.并求当t为何值时,四边形DEGF是平行四边形?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某苹果生产基地,用30名工人进行采摘或加工苹果 ,每名工人只能做其中一项工作.苹果的销售方式有两种:一种是可以直接出售;另一种是可以将采摘的苹果加工成罐头出售.直接出售每吨获利4 000元;加工成罐头出售每吨获利10 000元.采摘的工人每人可采摘苹果0.4吨;加工罐头的工人每人可加工0.3吨.设有x名工人进行苹果采摘,全部售出后,总利润为y元.
(1)求y与x的函数关系式;
(2)如何分配工人才能获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
拓展与延伸:
(1)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为__________________;
(2)如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ①
①  ②
② -
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种对正整数n的“F运算”:①当n为奇数时,结果为3n+5;②当n为偶数时,结果为
 (其中k是使
(其中k是使 为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
为奇数的最小正整数),并且运算重复进行.例如:取n=26,则运算过程如图:
那么当n=26时,第2016次“F运算”的结果是_____.
相关试题

