Question

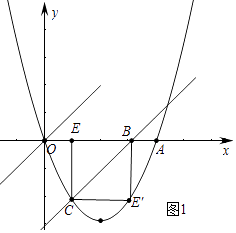
【题目】如图1，已知二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为﹣ ，直线l的解析式为y=x．

（1）求二次函数的解析式；
（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；
（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标．

Answer 1

【答案】
（1）

解：由题意抛物线的顶点坐标为（2，﹣ ），设抛物线的解析式为y=a（x﹣2）2﹣ ，

把（0，0）代入得到a= ，

∴抛物线的解析式为y= （x﹣2）2﹣ ，即y= x2﹣ x

（2）

解：如图1中，设E（m，0），则C（m， m2﹣ m），B（﹣ m2+ m，0），

∵E′在抛物线上，

∴E、B关于对称轴对称，

∴ =2，

解得m=1或6（舍弃），

∴B（3，0），C（1，﹣2），

∴直线l′的解析式为y=x﹣3

（3）

解：如图2中，

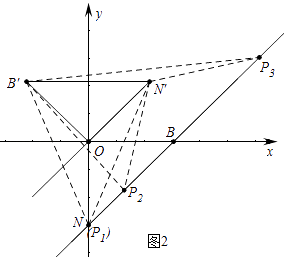
①当P1与N重合时，△P1B′N′是等腰三角形，此时P1（0，﹣3）．

②当N′=N′B′时，设P（m，m﹣3），

则有（m﹣ ）2+（m﹣3﹣ ）2=（3 ）2，

解得m= 或 ，

∴P2（ ， ），P3（ ， ）．

综上所述，满足条件的点P坐标为（0，﹣3）或（ ， ）或（ ， ）

【解析】（1）由题意抛物线的顶点坐标为（2，﹣ ），设抛物线的解析式为y=a（x﹣2）2﹣ ，把（0，0）代入得到a= ，即可解决问题；（2）如图1中，设E（m，0），则C（m， m2﹣ m），B（﹣ m2+ m，0），由E、B关于对称轴对称，可得 =2，由此即可解决问题；（3）分两种情形求解即可①当P1与N重合时，△P1B′N′是等腰三角形，此时P1（0，﹣3）．②当N′=N′B′时，设P（m，m﹣3），列出方程解方程即可；
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．