搜索
【题目】反比例函数y= 
的图象如图所示，则一次函数y=kx+b（k≠0）的图象的图象大致是（ ） 
A.
B.
C.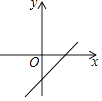
D.
参考答案：
【答案】D
【解析】解：∵y= 
的图象经过第一、三象限， ∴kb＞0，
∴k，b同号，
A、图象过二、四象限，
则k＜0，图象经过y轴正半轴，则b＞0，此时，k，b异号，故此选项不合题意；
B、图象过二、四象限，
则k＜0，图象经过原点，则b=0，此时，k，b不同号，故此选项不合题意；
C、图象过一、三象限，
则k＞0，图象经过y轴负半轴，则b＜0，此时，k，b异号，故此选项不合题意；
D、图象过一、三象限，
则k＞0，图象经过y轴正半轴，则b＞0，此时，k，b同号，故此选项符合题意；
故选：D．
【考点精析】根据题目的已知条件，利用一次函数的图象和性质和反比例函数的图象的相关知识可以得到问题的答案，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点E、G分别是边AD、BC的中点，AF=
AB．
（1）求证：EF⊥AG；
（2）若点F、G分别在射线AB、BC上同时向右、向上运动，点G运动速度是点F运动速度的2倍，EF⊥AG是否成立（只写结果，不需说明理由）？
（3）正方形ABCD的边长为4，P是正方形ABCD内一点，当S△PAB=S△OAB ， 求△PAB周长的最小值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知二次函数y=ax2+bx+c（a、b、c为常数，a≠0）的图象过点O（0，0）和点A（4，0），函数图象最低点M的纵坐标为﹣
，直线l的解析式为y=x．
（1）求二次函数的解析式；
（2）直线l沿x轴向右平移，得直线l′，l′与线段OA相交于点B，与x轴下方的抛物线相交于点C，过点C作CE⊥x轴于点E，把△BCE沿直线l′折叠，当点E恰好落在抛物线上点E′时（图2），求直线l′的解析式；
（3）在（2）的条件下，l′与y轴交于点N，把△BON绕点O逆时针旋转135°得到△B′ON′，P为l′上的动点，当△PB′N′为等腰三角形时，求符合条件的点P的坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法正确的是（ ）
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中，不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0（a≠0）一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE，则△ABC与△ADE不全等 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，PA切⊙O于点A，连结PO并延长交⊙O于点C，连结AC，AB=10，∠P=30°，则AC的长度是（ ）
A.
B.
C.5
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠BAC=60°，点O从A点出发，以2m/s的速度沿∠BAC的角平分线向右运动，在运动过程中，以O为圆心的圆始终保持与∠BAC的两边相切，设⊙O的面积为S（cm2），则⊙O的面积S与圆心O运动的时间t（s）的函数图象大致为（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论： ①抛物线过原点；
②4a+b+c=0；
③a﹣b+c＜0；
④抛物线的顶点坐标为（2，b）；
⑤当x＜2时，y随x增大而增大．
其中结论正确的是（ ）
A.①②③
B.③④⑤
C.①②④
D.①④⑤
相关试题
