【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.

(1)求证,![]() ;
;
(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;

(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)![]() ,见解析;(2)D(3,1),
,见解析;(2)D(3,1),![]() 平移的距离是
平移的距离是![]() 个单位,见解析;(3)存在满足条件的点Q,其坐标为
个单位,见解析;(3)存在满足条件的点Q,其坐标为![]() 或
或![]() 或
或![]() ,见解析.
,见解析.
【解析】
(1)根据AAS或ASA即可证明;
(2)首先求直线AB的解析式,再求出出点D的坐标,再求出直线B′C′的解析式,求出点C′的坐标即可解决问题;
(3)如图3中,作CP∥AB交y轴于P,作PQ∥CD交AB于Q,则四边形PCDQ是平行四边形,求出直线PC的解析式,可得点P坐标,点C向左平移1个单位,向上平移![]() 个单位得到P,推出点D向左平移1个单位,向上平移
个单位得到P,推出点D向左平移1个单位,向上平移![]() 个单位得到Q,再根据对称性可得Q′、Q″的坐标.
个单位得到Q,再根据对称性可得Q′、Q″的坐标.
(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
(2)∵直线AB与x轴,y轴交于![]() 、
、![]() 两点
两点
∴直线AB的解析式为![]()
∵![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]()
把![]() 代入
代入![]() 得到
得到![]() ,
,
∴![]()
∵![]() ,
,![]()
∴直线BC的解析式为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() 代入得到
代入得到![]()
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 平移的距离是
平移的距离是![]() 个单位.
个单位.
(3)如图3中,作CP∥AB交y轴于P,作PQ∥CD交AB于Q,则四边形PCDQ是平行四边形,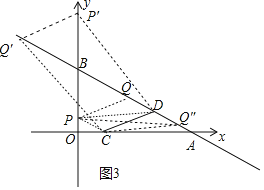
易知直线PC的解析式为y=-![]() x+
x+![]() ,
,
∴P(0,![]() ),
),
∵点C向左平移1个单位,向上平移![]() 个单位得到P,
个单位得到P,
∴点D向左平移1个单位,向上平移![]() 个单位得到Q,
个单位得到Q,
∴Q(2,![]() ),
),
当CD为对角线时,四边形PCQ″D是平行四边形,可得Q″![]() ,
,
当四边形CDP′Q′为平行四边形时,可得Q′![]() ,
,
综上所述, 存在满足条件的点Q,其坐标为![]() 或
或![]() 或
或![]()
-
科目: 来源: 题型:
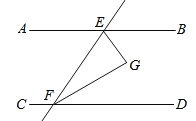
查看答案和解析>>【题目】如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,
(1)若∠AEF=50°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
-
科目: 来源: 题型:
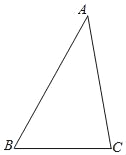
查看答案和解析>>【题目】如图,在△ABC中,BC=3
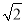 ,AC=5,∠B=45°,则下面结论正确的是_____.
,AC=5,∠B=45°,则下面结论正确的是_____.①∠C一定是钝角;
②△ABC的外接圆半径为3;
③sinA=
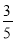 ;
;④△ABC外接圆的外切正六边形的边长是
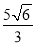 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠DAC=90°,△ABC是等边三角形,点P为射线AD上任意一点(点P与点A不重合),连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连接QB并延长交直线AD于E.

(1)如图1,猜想∠QEP= ;
(2)如图2,若当∠DAC是锐角时,其他条件不变,猜想∠QEP的度数,并证明;
(3)如图3,若∠DAC=135°,∠ACP=15°,且AC=6,求BQ的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 ,
, ,
,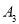 ,…在射线
,…在射线 上,点
上,点 ,
, ,
, ,…在射线
,…在射线 上,
上, ,
, ,
, ,…均为等边三角形,若
,…均为等边三角形,若 ,则
,则 的边长为( )
的边长为( )
A.8B.16C.24D.32
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
①
 的解x= .
的解x= .②
 的解x= .
的解x= .③
 的解x= .
的解x= .④
 的解x= .
的解x= .…
(1)根据你发现的规律直接写出⑤,⑥个方程及它们的解.
(2)请你用一个含正整数n的式子表示上述规律,并求出它的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为美化学校环境,建设绿色校园,陶治师生情操我校计划用180元购买A、B两种花卉苗共20棵,已知A种花卉苗每棵12元,B种花卉苗每棵8元.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
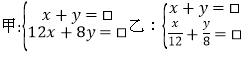
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示 ,y表示 ;
乙:x表示 ,y表示 ;
(2)求A、B两种花卉各多少棵?(写出完整的解答过程)
相关试题

