【题目】为美化学校环境,建设绿色校园,陶治师生情操我校计划用180元购买A、B两种花卉苗共20棵,已知A种花卉苗每棵12元,B种花卉苗每棵8元.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程组如下:
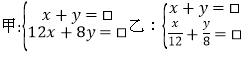
根据甲、乙两名同学所列的方程组,请你分别指出未知数x,y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:
甲:x表示 ,y表示 ;
乙:x表示 ,y表示 ;
(2)求A、B两种花卉各多少棵?(写出完整的解答过程)
参考答案:
【答案】(1)20,180,180,20,A种花卉苗棵数,B种花卉苗棵数,购买A种花卉苗总共的价钱,购买B种花卉苗总共的价钱;(2)A种花卉苗5棵,B种花卉苗15棵.
【解析】
(1)根据所列式子可知,甲同学方程所列方程组中未知数为:设A种花卉苗x棵,B种花卉苗y棵;乙同学所列方程组中未知数为:设购买A种花卉苗共用了x元,购买B种花卉苗共用了y元,据此补全方程组即可;
(2)选择其中一个方程组解答,即可解决问题.
解:(1)根据题意,甲:设A种花卉苗x棵,B种花卉苗y棵,则
列出方程组为:![]() ;
;
乙:设购买A种花卉苗共用了x元,购买B种花卉苗共用了y元,则
列出方程组为: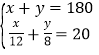 ;
;
故答案依次为:20,180,180,20,A种花卉苗棵数,B种花卉苗棵数,购买A种花卉苗总共的价钱,购买B种花卉苗总共的价钱;
(2)选甲同学所列方程组解答如下:
![]() ,解得:
,解得:![]() ,
,
∴A种花卉苗5棵,B种花卉苗15棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于
 、
、 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作 轴于点E.
轴于点E.
(1)求证,
 ;
;(2)如图2,将
 沿x轴正方向平移得
沿x轴正方向平移得 ,当直线
,当直线 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及 平移的距离;
平移的距离;
(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,点
,点 ,
, ,
,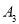 ,…在射线
,…在射线 上,点
上,点 ,
, ,
, ,…在射线
,…在射线 上,
上, ,
, ,
, ,…均为等边三角形,若
,…均为等边三角形,若 ,则
,则 的边长为( )
的边长为( )
A.8B.16C.24D.32
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
①
 的解x= .
的解x= .②
 的解x= .
的解x= .③
 的解x= .
的解x= .④
 的解x= .
的解x= .…
(1)根据你发现的规律直接写出⑤,⑥个方程及它们的解.
(2)请你用一个含正整数n的式子表示上述规律,并求出它的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠C=90°.
(1)用尺规作图作Rt△ABC的重心P.(保留作图痕迹,不要求写作法和证明);
(2)你认为只要知道Rt△ABC哪一条边的长即可求出它的重心与外心之间的距离?并请你说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】州教育局为了解我州八年级学生参加社会实践活动情况,随机抽查了某县部分八年级学生第一学期参加社会实践活动的天数,并用得到的数据检测了两幅统计图,下面给出了两幅不完整的统计图(如图)

请根据图中提供的信息,回答下列问题:
(1)a= %,并写出该扇形所对圆心角的度数为 ,请补全条形图.
(2)在这次抽样调查中,众数和中位数分别是多少?
(3)如果该县共有八年级学生2000人,请你估计“活动时间不少于7天”的学生人数大约有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图1,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图2,当EF与AB相交时,若∠EAB=α(0°<α<90°),请你直接写出线段EG、AG、BG之间的数量关系(用含α的式子表示);
(3)如图3,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.

相关试题

