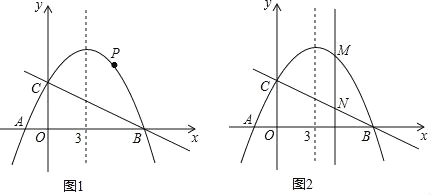
【题目】如图,已知抛物线y=ax2+![]() x+4的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点.
x+4的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点.
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标.
参考答案:
【答案】(1)![]() .点
.点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(2)存在点
;(2)存在点![]() ,使
,使![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .(3)
.(3)![]() 点的坐标为
点的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
【解析】
(1)由抛物线的对称轴为直线x=3,利用二次函数的性质即可求出a值,进而可得出抛物线的解析式,再利用二次函数图象上点的坐标特征,即可求出点A、B的坐标;
(2)利用二次函数图象上点的坐标特征可求出点C的坐标,由点B、C的坐标,利用待定系数法即可求出直线BC的解析式,假设存在,设点P的坐标为(x,-![]() x2+
x2+![]() x+4),过点P作PD∥y轴,交直线BC于点D,则点D的坐标为(x,-
x+4),过点P作PD∥y轴,交直线BC于点D,则点D的坐标为(x,-![]() x+4),PD=-
x+4),PD=-![]() x2+2x,利用三角形的面积公式即可得出S△PBC关于x的函数关系式,再利用二次函数的性质即可解决最值问题;
x2+2x,利用三角形的面积公式即可得出S△PBC关于x的函数关系式,再利用二次函数的性质即可解决最值问题;
(3)设点M的坐标为(m,-![]() m2+
m2+![]() m+4),则点N的坐标为(m,-
m+4),则点N的坐标为(m,-![]() m+4),进而可得出MN=|-
m+4),进而可得出MN=|-![]() m2+2m|,结合MN=3即可得出关于m的含绝对值符号的一元二次方程,解之即可得出结论.
m2+2m|,结合MN=3即可得出关于m的含绝对值符号的一元二次方程,解之即可得出结论.
(1)抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,
∴抛物线的解析式为![]() .
.
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(2)当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
将![]() 、
、![]() 代入
代入![]() ,
,
![]() ,解得:
,解得: ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
假设存在,设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点
于点![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,如图所示.
,如图所示.
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴当![]() 时,
时,![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .
.
∵![]() ,
,
∴存在点![]() ,使
,使![]() 的面积最大,最大面积是
的面积最大,最大面积是![]() .
.
(3)设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
当![]() 时,有
时,有![]() ,
,
解得:![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
当![]() 或
或![]() 时,有
时,有![]() ,
,
解得:![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
综上所述:![]() 点的坐标为
点的坐标为![]() 、
、![]() 、
、![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

-
科目: 来源: 题型:
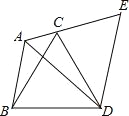
查看答案和解析>>【题目】已知:如图,在△ABC中,∠BAC=120°,以BC为边向形外作等边三角形BCD,把△ABD绕着点D按顺时针方向旋转60°后得到△ECD,若AB=5,AC=3,求∠BAD的度数与AD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司试销一种成本单价为50元/件的新产品,规定试销时销售单价不低于成本单价,又不高于80元/件,经试销调查,发现销售量y(件)与销售单价x(元/件)可近似看作一次函数y=kx+b的关系(如图所示)
(I)根据图象,求一次函数y=kx+b的解析式,并写出自变量x的取值范围;
(Ⅱ)该公司要想每天获得最大的利润,应把销售单价定为多少?最大利润值为多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF,在
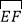 上取动点G,国点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
上取动点G,国点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
A. 正比例函数y=kx(k为常数,k≠0,x>0)
B. 一次函数y=kx+b(k,b为常数,kb≠0,x>0)
C. 反比例函数y=
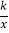 (k为常数,k≠0,x>0)
(k为常数,k≠0,x>0)D. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为5,l2与l3的距离为7,则Rt△ABC的面积为___________

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下内容,再解决问题.
在把多项式m2﹣4mn﹣12n2进行因式分解时,虽然它不符合完全平方公式,但是经过变形,可以利用完全平方公式进行分解:
m2﹣4mn﹣12n2=m2﹣4mn+4n2﹣4n2﹣12n2=(m﹣2n)2﹣16n2=(m﹣6n)(m+2n),像这样构造完全平方式的方法我们称之为“配方法”,利用这种方法解决下面问题.
(1)把多项式因式分解:a2﹣6ab+5b2;
(2)已知a、b、c为△ABC的三条边长,且满足4a2﹣4ab+2b2+3c2﹣4b﹣12c+16=0,试判断△ABC的形状.
相关试题

