搜索
【题目】阅读下内容，再解决问题．
在把多项式m2﹣4mn﹣12n2进行因式分解时，虽然它不符合完全平方公式，但是经过变形，可以利用完全平方公式进行分解：
m2﹣4mn﹣12n2＝m2﹣4mn+4n2﹣4n2﹣12n2＝（m﹣2n）2﹣16n2＝（m﹣6n）（m+2n），像这样构造完全平方式的方法我们称之为“配方法”，利用这种方法解决下面问题．
（1）把多项式因式分解：a2﹣6ab+5b2；
（2）已知a、b、c为△ABC的三条边长，且满足4a2﹣4ab+2b2+3c2﹣4b﹣12c+16＝0，试判断△ABC的形状．
参考答案：
【答案】（1）（a﹣b）（a﹣5b）；（2）△ABC为等腰三角形
【解析】
（1）根据完全平方公式、平方差公式解答；
（2）先根据完全平方公式把原式变形，再根据偶次方的非负性分别求出a、b、c，然后根据等腰三角形的定义解答即可．
（1）
；
（2）
由偶次方的非负性得：
解得：
为等腰三角形．
-
科目： 来源： 题型：
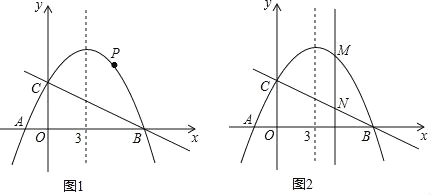
查看答案和解析>>【题目】如图，已知抛物线y=ax2+
x+4的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．（1）求抛物线的解析式和A、B两点的坐标；
（2）若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；
（3）若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是定长线段，圆心O是AB的中点，AE、BF为切线，E、F为切点，满足AE=BF，在
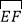上取动点G，国点G作切线交AE、BF的延长线于点D、C，当点G运动时，设AD=y，BC=x，则y与x所满足的函数关系式为（ ）
A. 正比例函数y=kx（k为常数，k≠0，x＞0）
B. 一次函数y=kx+b（k，b为常数，kb≠0，x＞0）
C. 反比例函数y=
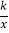（k为常数，k≠0，x＞0）D. 二次函数y=ax2+bx+c（a，b，c为常数，a≠0，x＞0）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，Rt△ABC中，∠ABC＝90°，AB＝BC，直线l1、l2、l3分别通过A、B、C三点，且l1∥l2∥l3．若l1与l2的距离为5，l2与l3的距离为7，则Rt△ABC的面积为___________
-
科目： 来源： 题型：
查看答案和解析>>【题目】在利用构造全等三角形来解决的问题中，有一种典型的利用倍延中线的方法，例如：在△ABC中，AB＝8，AC＝6，点D是BC边上的中点，怎样求AD的取值范围呢？我们可以延长AD到点E，使AD＝DE，然后连接BE（如图①），这样，在△ADC和△EDB中，由于
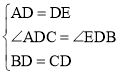，∴△ADC≌△EDB，∴AC＝EB，接下来，在△ABE中通过AE的长可求出AD的取值范围．请你回答：
（1）在图①中，中线AD的取值范围是 ．
（2）应用上述方法，解决下面问题
①如图②，在△ABC中，点D是BC边上的中点，点E是AB边上的一点，作DF⊥DE交AC边于点F，连接EF，若BE＝4，CF＝2，请直接写出EF的取值范围．
②如图③，在四边形ABCD中，∠BCD＝150°，∠ADC＝30°，点E是AB中点，点F在DC上，且满足BC＝CF，DF＝AD，连接CE、ED，请判断CE与ED的位置关系，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】八年级（1）班研究性学习小组为研究全校同学课外阅读情况，在全校随机邀请了部分同学参与问卷调查，统计同学们一个月阅读课外书的数量，并绘制了以下统计图．
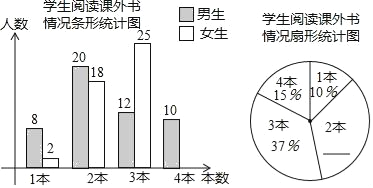
请根据图中信息解决下列问题：
（1）共有 名同学参与问卷调查；
（2）补全条形统计图和扇形统计图；
（3）全校共有学生1500人，请估计该校学生一个月阅读2本课外书的人数约为多少．
-
科目： 来源： 题型：
查看答案和解析>>【题目】跳远运动员李阳对训练效果进行测试．6次跳远的成绩如下：7.5，7.7，7.6，7.7，7.9，7.8（单位：m）这六次成绩的平均数为7.7m，方差为
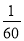．如果李阳再跳一次，成绩为7.7m．则李阳这7次跳远成绩的方差_____（填“变大”、“不变”或“变小”）．
相关试题
