Question

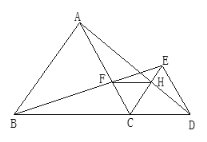
【题目】如图，已知点B、C、D在同一条直线上，△ABC和△CDE都是等边三角形．BE交AC于F，AD交CE于H，

(1)求证：△BCE≌△ACD；

(2)求证：FC=HC

(3)求证：FH∥BD．

Answer 1

【答案】（1）详见解析；（2）详见解析；（3）详见解析.

【解析】

（1）先根据△ABC和△CDE都是等边三角形得出BC=AC，CE=CD，∠BCA=∠ECD=60°，再由SAS定理即可得出△BCE≌△ACD；

（2）由△BCE ≌ △ACD，可得∠CBF=∠CAH，然后根据“ASA”证明△BCF≌△ACH即可；

（3）根据∠FCH=60°，可知△CHF为等边三角形，进而可得出结论．

（1）∵△ABC和△CDE都是等边三角形，

∴BC=AC，CE=CD，∠BCA=∠ECD=60°，

∴∠BCA+∠ACE=∠ECD+∠ACE，即∠BCE=∠ACD，

∴在△BCE和△ACD中，

BC＝AC∠BCE＝∠ACDCE＝CD，

∴△BCE ≌ △ACD（SAS）．

（2）∵△BCE ≌ △ACD，

∴∠CBF=∠CAH，

又∵△ABC和△CDE都是等边三角形，且点B、C、D在同一条直线上，

∴∠ACH=180°-∠ACB-∠HCD=60°=∠BCF，

在△BCF和△ACH中，

∠CBE＝∠CAHBC＝AC∠BCF＝∠ACH，

∴△BCF≌△ACH（ASA），

∴CF=CH，

（3）∵∠FCH=60°，

∴△CHF为等边三角形

∴∠FHC=∠HCD=60°，

∴FH∥BD．