【题目】如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=![]() ,CD=2
,CD=2![]() ,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2
,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2![]() ;④AE=
;④AE=![]() .其中正确的结论是( )
.其中正确的结论是( )
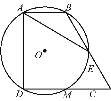
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
参考答案:
【答案】B
【解析】
连接BD,BM,AM,EM,DE,利用三个角为直角的四边形为矩形得到ABMD为矩形,利用矩形的对边相等得到AB=DM,进而可证明DM=CM,故选项①正确;在Rt△DEC中,由M为CD的中点,利用斜边上的中线等于斜边的一半得到DM与EM相等,从而AB=EM,所以弧AB=弧EM,故选项②正确;先证明四边形AMCB为平行四边形,可得出AM=BC,等量代换得到BC=BD,由BD为圆的直径,可得△DEC为直角三角形,利用勾股定理可求出DE的长,设BE=x,则BD=BC=BE+EC=x+2,在Rt△BDE中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出BC的长,即为BD的长,确定出圆的直径,即可对于选项③作出判断;在Rt△AEM中,由AM与ME的长,利用勾股定理求出AE的长,即可对于选项④作出判断.
连接BD,BM,AM,EM,DE,
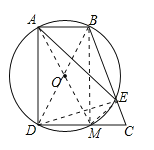
∵∠BAD=90°,
∴BD为圆的直径,
∴∠BMD=90°,
∴∠BAD=∠CDA=∠BMD=90°,
∴四边形ABMD矩形,
∴AB=DM,
又∵CD=2AB,
∴CD=2DM,即DM=MC;
故选项①正确;
在Rt△DEC中,M是DC中点,
∴EM=DM=![]() CD=
CD=![]() ,
,
∴弧EM=弧DM,
又∵AB=DM,
∴弧AB=弧DM,
∴弧AB=弧EM,
故选项②正确;
∵AB∥MC,AB=MC,
∴四边形ABCM是平行四边形,
∴AM=BC,又BD=AM,
∴BD=BC,
∵BD是直径,
∴∠BED=90°,即∠DEC=90°,
又EC=2,DC=2![]() ,
,
根据勾股定理得:DE=![]() =2
=2![]() ,
,
设BE=x,BD=BC=BE+EC=x+2,
在Rt△BDE中,根据勾股定理得:BE2+DE2=BD2,即x2+20=(x+2)2,
解得:x=4,
∴BD=6,故选项③错误;
在Rt△AEM中,AM=6,EM=![]() ,
,
根据勾股定理得:AE=![]() =
=![]() ;
;
故选项④正确;
则正确的选项为:①②④.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论:①b2-4ac<0;②ab>0;③a-b+c=0;④4a+b=0;⑤当y=2时,x只能等于0.其中正确的是( )
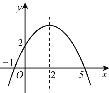
A. ①④ B. ③④ C. ②⑤ D. ③⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AC的垂直平分线DE与∠ABC的角平分线相交于点D,垂足为点E,若∠ABC=72°,求∠ADC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017湖北省恩施州)如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=
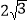 ,则图中阴影部分的面积为______.(结果不取近似值)
,则图中阴影部分的面积为______.(结果不取近似值)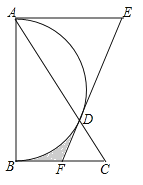
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 、
、 和线段
和线段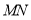 都在数轴上,点
都在数轴上,点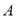 、
、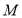 、
、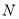 、
、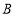 对应的数字分别为
对应的数字分别为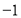 、0、2、11.线段
、0、2、11.线段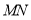 沿数轴的正方向以每秒1个单位的速度移动,设移动时间为
沿数轴的正方向以每秒1个单位的速度移动,设移动时间为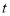 秒.
秒.
(1)
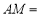 __________;(用含有
__________;(用含有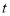 的代数式表示.)
的代数式表示.)(2)当
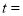 _________秒时,
_________秒时,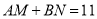 ;
;(3)若点
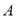 、
、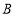 与线段
与线段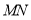 同时移动,点
同时移动,点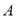 以每秒2个单位长度的速度向数轴的正方向移动,点
以每秒2个单位长度的速度向数轴的正方向移动,点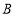 以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,当
以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,当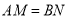 时,
时,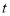 的值为__________.
的值为__________.
相关试题

