【题目】如图,已知![]() 、
、![]() 和线段
和线段![]() 都在数轴上,点
都在数轴上,点![]() 、
、![]() 、
、![]() 、
、![]() 对应的数字分别为
对应的数字分别为![]() 、0、2、11.线段
、0、2、11.线段![]() 沿数轴的正方向以每秒1个单位的速度移动,设移动时间为
沿数轴的正方向以每秒1个单位的速度移动,设移动时间为![]() 秒.
秒.

(1)![]() __________;(用含有
__________;(用含有![]() 的代数式表示.)
的代数式表示.)
(2)当![]() _________秒时,
_________秒时,![]() ;
;
(3)若点![]() 、
、![]() 与线段
与线段![]() 同时移动,点
同时移动,点![]() 以每秒2个单位长度的速度向数轴的正方向移动,点
以每秒2个单位长度的速度向数轴的正方向移动,点![]() 以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,当
以每秒1个单位长度的速度向数轴的负方向移动.在移动过程中,当![]() 时,
时,![]() 的值为__________.
的值为__________.
参考答案:
【答案】(1)![]() ;(2)9.5;(3)
;(2)9.5;(3)![]() 或8.
或8.
【解析】
(1)根据点M开始表示的数结合其运动速度和时间,即可得出运动后点M的表示的数,再依据点A表示的数为﹣1即可得出结论;
(2)分别找出AM、BN,根据AM+BN=11即可列出关于t的含绝对值符号的一元一次方程,解方程即可得出结论;
(3)假设能够相等,找出AM、BN,根据AM=BN即可列出关于t的含绝对值符号的一元一次方程,解方程即可得出结论.
解:(1)∵点A、M、N对应的数字分别为﹣1、0、2,线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒,
∴移动后M表示的数为t,N表示的数为t+2,
∴AM=t﹣(﹣1)=t+1.
故答案为:t+1.
(2)∵MN在数轴上移动,AB=12,MN=2,
∴当MN在AB中间时,AM+NB=AB﹣MN=10<11,
∴要使AM+NB=11,则MN应在B点右侧,此时AM=1+t,NB=t﹣9,
∴AM+NB=1+t+t﹣9=2t﹣8=11,
解得:t=9.5.
故答案为:9.5.
(3)假设能相等,则点A表示的数为2t﹣1,M表示的数为t,N表示的数为t+2,B表示的数为11﹣t,
∴AM=|2t﹣1﹣t|=|t﹣1|,BN=|t+2﹣(11﹣t)|=|2t﹣9|,
∵AM=BN,
∴|t﹣1|=|2t﹣9|,
解得:t1=![]() ,t2=8.
,t2=8.
故在运动的过程中AM和BN能相等,此时运动的时间为![]() 秒或8秒
秒或8秒
故答案是:![]() 或8.
或8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角梯形ABCD中,∠BAD=∠CDA=90°,AB=
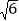 ,CD=2
,CD=2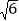 ,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2
,过A,B,D三点的☉O分别交BC,CD于点E,M,且CE=2,下列结论:①DM=CM;②弧AB=弧EM;③☉O的直径为2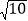 ;④AE=
;④AE=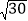 .其中正确的结论是( )
.其中正确的结论是( )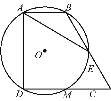
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017湖北省恩施州)如图,在Rt△ABC中,∠BAC=30°,以直角边AB为直径作半圆交AC于点D,以AD为边作等边△ADE,延长ED交BC于点F,BC=
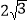 ,则图中阴影部分的面积为______.(结果不取近似值)
,则图中阴影部分的面积为______.(结果不取近似值)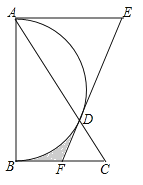
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的顶角为36°,则这个三角形就是黄金三角形。如图,在△ABC中,BA=BC,D 在边 CB 上,且 DB=DA=AC。

(1)如图1,写出图中所有的黄金三角形,并证明;
(2)若 M为线段 BC上的点,过 M作直线MH⊥AD于 H,分别交直线 AB,AC与点N,E,如图 2,试写出线段 BN、CE、CD之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是等边
 内一点
内一点 将
将 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转 得
得 ,连接
,连接 已知
已知
 .
. 求证:
求证: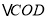 是等边三角形;
是等边三角形; 当
当 时,试判断
时,试判断 的形状,并说明理由;
的形状,并说明理由; 探究:当
探究:当 为多少度时,
为多少度时, 是等腰三角形.
是等腰三角形.
-
科目: 来源: 题型:
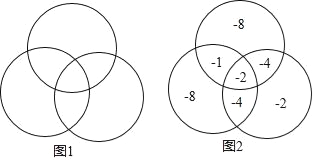
查看答案和解析>>【题目】现有七个数﹣1,﹣2,﹣2,﹣4,﹣4,﹣8,﹣8将它们填入图1(3个圆两两相交分成7个部分)中,使得每个圆内部的4个数之积相等,设这个积为m,如图2给出了一种填法,此时m=64,在所有的填法中,m的最大值为_____.
相关试题

