搜索
【题目】如图,△ABC中,CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M,若CM=5,求
+
的值.
参考答案：
【答案】100
【解析】
根据角平分线的定义可以证明出△CEF是直角三角形，再根据平行线的性质以及角平分线的定义证明得到EM=CM=MF然后求出EF的长度，然后利用勾股定理列式计算即可求解．
解：∵CE平分∠ACB交AB于E，CF平分∠ACD，
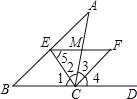
∴∠1=∠2=
∠ACB,∠3=∠4=∠ACD，
∴∠2+∠3= (∠ACB+∠ACD)=90°，
∴△CEF是直角三角形，
∵EF∥BC，
∴∠1=∠5，∠4=∠F，
∴∠2=∠5，∠3=∠F，
∴EM=CM，CM=MF，
∵CM=5，
∴EF=5+5=10，
在Rt△CEF中, 
=100.
故答案为：100.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A. B. C的坐标分别为(1,0)、(2,3)、(3,1).
(1)作出△ABC关于x轴对称的△A1 B1 C1,并写出B1的坐标：B1(___,___)
(2)在y轴上找一点D，使得BD+DA的值最小，D点的坐标______.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系
中，正方形ABCO的对角线BO在x 轴上，若正方形ABCO的边长为
，点B在x负半轴上，反比例函数
的图象经过C点．（1）求该反比例函数的解析式；
（2）当函数值
＞-2时，请直接写出自变量x的取值范围；（3）若点P是反比例函数上的一点，且△PBO的面积恰好等于正方形ABCO的面积，求点P的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】近年来，共享单车服务的推出（如图1），极大的方便了城市公民绿色出行，图2是某品牌某型号单车的车架新投放时的示意图（车轮半径约为30cm），其中BC∥直线l，∠BCE=71°，CE=54cm．
（1）求单车车座E到地面的高度；（结果精确到1cm）
（2）根据经验，当车座E到CB的距离调整至等于人体胯高（腿长）的0.85时，坐骑比较舒适．小明的胯高为70cm，现将车座E调整至座椅舒适高度位置E′，求EE′的长．（结果精确到0.1cm）
（参考数据：sin71°≈0.95，cos71°≈0.33，tan71°≈2.90）
-
科目： 来源： 题型：
查看答案和解析>>【题目】点P是∠AOB的内部任意一点，PM⊥OA，PN⊥OB，垂足分别是M、N，D是OP的中点
（1）求证：DM=DN
（2）连接MN,当∠MPN=______时，△DMN是等边三角形；
（3）探索∠MPN与∠MDN的数量关系，并说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】长方形ABCD中，AB=6，AD=8，点E为边AD上一点，将△ABE沿BE折叠后得到△BEF．
（1）如图1，若点E为AD的中点，延长BF交边CD于点G．
①求证：DG=FG．
②求FG的长度．
（2）如图2，若点E为边AD的一动点，连接FD，△DEF能否为直角三角形？若能，求出AE的值．若不能，请说明理由．
相关试题
