【题目】
(1)解方程: ![]() +
+ ![]() =2
=2
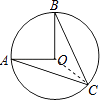
(2)如图,在⊙O中,OA⊥OB,∠A=20°,求∠B的度数.
参考答案:
【答案】
(1)解:去分母得,1﹣(x+2)=2(x﹣2),
去括号得,1﹣x﹣2=2x﹣4,
移项得,﹣x﹣2x=﹣4﹣1+2,
合并同类项得,﹣3x=﹣3,
系数化为1得,x=1,
经检验,x=1是原方程的解
(2)解:连接OC,
∵OA⊥OB,
∴∠AOB=90°,
∴∠ACB=45°.
又∴OA=OC,∠A=20°,
∴∠ACO=20°,
∴∠OCB=25°.
又∵OC=OB
∴∠B=25°.
【解析】(1)先把分式方程化为整式方程,求出x的值,再代入最简公分母进行检验即可;(2)连接OC,先根据圆周角定理求出∠ACB的度数,再由等腰三角形的性质求出∠ACO的度数,进而可得出∠BCO的度数,据此可得出结论.
【考点精析】通过灵活运用去分母法和圆周角定理,掌握先约后乘公分母,整式方程转化出.特殊情况可换元,去掉分母是出路.求得解后要验根,原留增舍别含糊;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(﹣6,8),C(﹣6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电动车厂平均每天计划生产200辆电动车,由于各种原因实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负)
星期
一
二
三
四
五
六
日
增减情况
+5
-2
-4
+13
-10
+16
-9
(1)产量最多的一天比产量最少的一天多生产多少辆?
(2)根据记录可知前五天共生产多少辆?
(3)该厂实行计件工资制,每辆车100元,超额完成则超额部分每辆车再奖励40元(以一周为单位结算),那么该厂工人这一周的工资总额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为a的正方形ABCD中,E、F是边AD,AB上两点(与端点不重合),且AE=BF.连接CE,DF相交于点M,
(1)当E为边AD的中点时,则DF的长为 (用含a的式子表示)
(2)求证:∠MCB+∠MFB=180°.
(3)点M能成为DF的中点吗?如果能,求出此时CM的长(用含a的式子表示);如果不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=
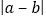 .
.
利用数轴,根据数形结合思想,回答下列问题:
(1)数轴上表示2和6两点之间的距离是_____ ,数轴上表示1和
 的两点之间的距离为__________
的两点之间的距离为__________(2)数轴上表示
 和1两点之间的距离为_____,数轴上表示
和1两点之间的距离为_____,数轴上表示 和
和 两点之间的距离为_________
两点之间的距离为_________(3)若
 表示一个实数,且
表示一个实数,且 ,化简
,化简 ,
,(4)
 的最小值为_______ ,
的最小值为_______ , 的最小值为__________ .
的最小值为__________ .(5)
 的最大值为__________
的最大值为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲种铅笔每支0.4元,乙种铅笔每支0.6元,某同学共购买了这两种铅笔30支,并且买乙种铅笔所花的钱是买甲种铅笔所花的钱的3倍.
(1)该同学购买甲乙两种铅笔各多少支?
(2)求该同学购买这两种铅笔共花了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=b,移在动过程中,双曲线y=
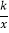 (x>0)的图象始终经过BC的中点E,交AB于点D.
(x>0)的图象始终经过BC的中点E,交AB于点D. 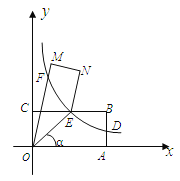
(1)证明:点D是AB的中点;
(2) 连结OE记∠AOE= α.
①当α=45°时,求 a、b之间的数量关系;
②当α=30°,k=
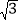 时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边形OMNE除点E外的另一个交点为F,求直线DF的解析式
相关试题

