【题目】如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=b,移在动过程中,双曲线y=![]() (x>0)的图象始终经过BC的中点E,交AB于点D.
(x>0)的图象始终经过BC的中点E,交AB于点D.
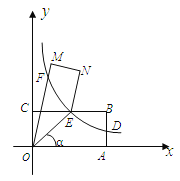
(1)证明:点D是AB的中点;
(2) 连结OE记∠AOE= α.
①当α=45°时,求 a、b之间的数量关系;
②当α=30°,k=![]() 时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
形OMNE除点E外的另一个交点为F,求直线DF的解析式
参考答案:
【答案】(1)见解析 (2)① a=2b ②![]()
【解析】分析:(1)根据中点坐标公式得到E点坐标,再根据待定系数法得到双曲线解析式,把D点的横坐标代入可求D点的纵坐标,依此即可证明;
(2)①根据等腰直角三角形的性质即可得到a、b之间的数量关系;
②首先过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,由∠EOA=30°,k=![]() ,即可求得点E的坐标,又由点E是BC的中点,可求得点D的横坐标,继而求得点D的坐标,然后由折叠的性质,可得∠FOA=60°,即可求得点F的坐标,然后由待定系数法求得直线DF的解析式.
,即可求得点E的坐标,又由点E是BC的中点,可求得点D的横坐标,继而求得点D的坐标,然后由折叠的性质,可得∠FOA=60°,即可求得点F的坐标,然后由待定系数法求得直线DF的解析式.
详解: ![]() ,
,
![]() ,
,
![]() ,得:
,得:![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() .
.
![]() =
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
![]() (3)如图,过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,
(3)如图,过点E作EH⊥OA于点H,过点F作FG⊥OA于点G,
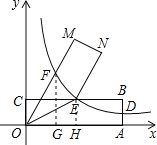
∵∠AOE=30°,k=![]() ,
,
∴![]() =
=![]() ,
,
∴OH=![]() EH,
EH,
∵S△EOH=![]() OHEH=
OHEH=![]() k=
k=![]() ,
,
∴EH=1,OH=![]() ,
,
∵E是BC的中点,
∴OA=2OH=2![]() ,
,
∴点D的横坐标为2![]() ,
,
则y=![]() ,
,
∴点D(2![]() ,
,![]() ),
),
由折叠的性质可得:∠FOA=2∠AOE=60°,
∴FG:OG=![]() ,
,
∵S△FOG=![]() OGFG=
OGFG=![]() k═
k═![]() ,
,
∴OG=1,FG=![]() ,
,
∴点F(1,![]() ),
),
设直线EF的解析式为:y=ax+b,
则 ,
,
解得: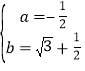 ,
,
∴直线EF的解析式为:y=![]() x+
x+![]() +
+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)解方程: +
+  =2
=2
(2)如图,在⊙O中,OA⊥OB,∠A=20°,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=
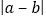 .
.
利用数轴,根据数形结合思想,回答下列问题:
(1)数轴上表示2和6两点之间的距离是_____ ,数轴上表示1和
 的两点之间的距离为__________
的两点之间的距离为__________(2)数轴上表示
 和1两点之间的距离为_____,数轴上表示
和1两点之间的距离为_____,数轴上表示 和
和 两点之间的距离为_________
两点之间的距离为_________(3)若
 表示一个实数,且
表示一个实数,且 ,化简
,化简 ,
,(4)
 的最小值为_______ ,
的最小值为_______ , 的最小值为__________ .
的最小值为__________ .(5)
 的最大值为__________
的最大值为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲种铅笔每支0.4元,乙种铅笔每支0.6元,某同学共购买了这两种铅笔30支,并且买乙种铅笔所花的钱是买甲种铅笔所花的钱的3倍.
(1)该同学购买甲乙两种铅笔各多少支?
(2)求该同学购买这两种铅笔共花了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
A. 2 B.
 C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的不等式组
 .
.
(1)当a=3时,解这个不等式组;
(2)若不等式组的解集是x<1,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某体育老师对自己任教的55名男生进行一百米摸底测试,若规定男生成绩为16秒合格,下表是随机抽取的10名男生分A、B两组测试的成绩与合格标准的差值(比合格标准多的秒数为正,少的秒数为负).
A 组
﹣1.5
+1.5
﹣1
﹣2
﹣2
B组
+1
+3
﹣3
+2
﹣3
(1)请你估算从55名男生中合格的人数大约是多少?
(2)通过相关的计算,说明哪个组的成绩比较均匀;
(3)至少举出三条理由说明A组成绩好于B组成绩,或找出一条理由来说明B组好于A组.
相关试题

