【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=![]() .
.
![]()
利用数轴,根据数形结合思想,回答下列问题:
(1)数轴上表示2和6两点之间的距离是_____ ,数轴上表示1和![]() 的两点之间的距离为__________
的两点之间的距离为__________
(2)数轴上表示![]() 和1两点之间的距离为_____,数轴上表示
和1两点之间的距离为_____,数轴上表示![]() 和
和![]() 两点之间的距离为_________
两点之间的距离为_________
(3)若![]() 表示一个实数,且
表示一个实数,且![]() ,化简
,化简![]() ,
,
(4)![]() 的最小值为_______ ,
的最小值为_______ ,
![]() 的最小值为__________ .
的最小值为__________ .
(5)![]() 的最大值为__________
的最大值为__________
![]()
参考答案:
【答案】(1)4; 3(2)![]() ,
,![]() ;(3)8;(4)7, 6;(5)4.
;(3)8;(4)7, 6;(5)4.
【解析】
(1)根据数轴上两点间的距离等于这两个数的差的绝对值列式计算即可得出结论;(2)根据数轴上两点的距离等于这两个数的差的绝对值列式即可得出结论;(3)根据绝对值的性质化简即可得出结论;(4)结合数轴,根据绝对值几何意义可得最小值;(5)根据绝对值非负的性质可得最大值.
解:(1)数轴上表示2和6两点之间的距离![]() ,
,
数轴上表示1和![]() 的两点之间的距离
的两点之间的距离![]() ;
;
(2)数轴上表示![]() 和1两点之间的距离
和1两点之间的距离![]() ,
,
数轴上表示![]() 和
和![]() 两点之间的距离
两点之间的距离![]() ;
;
(3)∵![]() ,
,
∴![]() ;
;
(4)∵![]() 的几何意义为
的几何意义为![]() 到-3与
到-3与![]() 到4的距离和,
到4的距离和,
∴![]() 取最小值时,
取最小值时,![]() 在-3与4之间,即最小值
在-3与4之间,即最小值![]() ,
,
同理可得![]() 的最小值为6;
的最小值为6;
(5)∵![]() 取最大值时,
取最大值时,![]() 最小,
最小,
∴![]() ,
,![]() ,
,
∴![]() 最大值
最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电动车厂平均每天计划生产200辆电动车,由于各种原因实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负)
星期
一
二
三
四
五
六
日
增减情况
+5
-2
-4
+13
-10
+16
-9
(1)产量最多的一天比产量最少的一天多生产多少辆?
(2)根据记录可知前五天共生产多少辆?
(3)该厂实行计件工资制,每辆车100元,超额完成则超额部分每辆车再奖励40元(以一周为单位结算),那么该厂工人这一周的工资总额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,边长为a的正方形ABCD中,E、F是边AD,AB上两点(与端点不重合),且AE=BF.连接CE,DF相交于点M,
(1)当E为边AD的中点时,则DF的长为 (用含a的式子表示)
(2)求证:∠MCB+∠MFB=180°.
(3)点M能成为DF的中点吗?如果能,求出此时CM的长(用含a的式子表示);如果不能,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)解方程: +
+  =2
=2
(2)如图,在⊙O中,OA⊥OB,∠A=20°,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲种铅笔每支0.4元,乙种铅笔每支0.6元,某同学共购买了这两种铅笔30支,并且买乙种铅笔所花的钱是买甲种铅笔所花的钱的3倍.
(1)该同学购买甲乙两种铅笔各多少支?
(2)求该同学购买这两种铅笔共花了多少元钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、C分别在x轴、y轴的正半轴上移动,过点O、A、C作矩形OABC,OA=a,OC=b,移在动过程中,双曲线y=
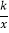 (x>0)的图象始终经过BC的中点E,交AB于点D.
(x>0)的图象始终经过BC的中点E,交AB于点D. 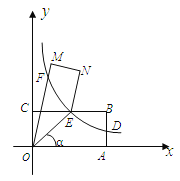
(1)证明:点D是AB的中点;
(2) 连结OE记∠AOE= α.
①当α=45°时,求 a、b之间的数量关系;
②当α=30°,k=
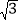 时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边
时,将四边形OABE沿OE翻折,得四边形OMNE,记双曲线与四边形OMNE除点E外的另一个交点为F,求直线DF的解析式
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
A. 2 B.
 C.
C.  D.
D. 
相关试题

