【题目】如图,边长为a的正方形ABCD中,E、F是边AD,AB上两点(与端点不重合),且AE=BF.连接CE,DF相交于点M,
(1)当E为边AD的中点时,则DF的长为 (用含a的式子表示)
(2)求证:∠MCB+∠MFB=180°.
(3)点M能成为DF的中点吗?如果能,求出此时CM的长(用含a的式子表示);如果不能,说明理由.

参考答案:
【答案】(1)![]() (2)见解析(3)不能
(2)见解析(3)不能
【解析】分析:(1)当E为边AD的中点时,则F也是AB的中点,在Rt△ADF中,利用勾股定理求出DF的长;
(2)首先利用全等三角形的判定方法利用SAS证明△ADF≌△DCE,得到∠ADF=∠DCE,进而得出∠DME=90°,于是得到结论;
(3)假设点M成为DF的中点,利用垂直平分线的性质得到DC=CF,进而得到结论与题意不符.
详解:(1)∵E为边AD的中点,
∴F也为边AB边的中点,
∴AF=![]() AB=
AB=![]() a,
a,
在Rt△ADF中,
AD2+AF2=DF2,
∴DF=![]() ;
;
(2)∵在正方形ABCD中,
∴AB=BC=CD=AD,
又∵AE=BF,
∴AF=DE,
∵∠CDE=∠A=90°,
∴△ADF≌△DCE,
∴∠ADF=∠DCE,
∵∠DCE+∠DEC=90°,
∴∠ADF+∠DEC=90°,
∴∠DME=90°,
∴∠MCB+∠MFB=180°;
(3)假设点M成为DF的中点,
∵∠DME=90°,
∴DF⊥CE,
∵M成为DF的中点,
∴CM是DF的垂直平分线,
∴DC=CF,
∵DC=BC≠CF,
∴点M不能成为DF的中点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
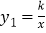 的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。
的图像和一次函数y2=ax+b的图像交于A(3,4)、B(—6,n)。
(1)求两个函数的解析式;
(2)观察图像,写出当x为何值时y1>y2?
(3)C、D分别是反比例函数
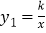 第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标.
第一、三象限的两个分支上的点,且以A、B、C、D为顶点的四边形是平行四边形.请直接写出C、D两点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(﹣6,8),C(﹣6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电动车厂平均每天计划生产200辆电动车,由于各种原因实际每天的生产量与计划量相比有出入.下表是某周的生产情况(超产为正,减产为负)
星期
一
二
三
四
五
六
日
增减情况
+5
-2
-4
+13
-10
+16
-9
(1)产量最多的一天比产量最少的一天多生产多少辆?
(2)根据记录可知前五天共生产多少辆?
(3)该厂实行计件工资制,每辆车100元,超额完成则超额部分每辆车再奖励40元(以一周为单位结算),那么该厂工人这一周的工资总额是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)解方程: +
+  =2
=2
(2)如图,在⊙O中,OA⊥OB,∠A=20°,求∠B的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=
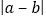 .
.
利用数轴,根据数形结合思想,回答下列问题:
(1)数轴上表示2和6两点之间的距离是_____ ,数轴上表示1和
 的两点之间的距离为__________
的两点之间的距离为__________(2)数轴上表示
 和1两点之间的距离为_____,数轴上表示
和1两点之间的距离为_____,数轴上表示 和
和 两点之间的距离为_________
两点之间的距离为_________(3)若
 表示一个实数,且
表示一个实数,且 ,化简
,化简 ,
,(4)
 的最小值为_______ ,
的最小值为_______ , 的最小值为__________ .
的最小值为__________ .(5)
 的最大值为__________
的最大值为__________
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲种铅笔每支0.4元,乙种铅笔每支0.6元,某同学共购买了这两种铅笔30支,并且买乙种铅笔所花的钱是买甲种铅笔所花的钱的3倍.
(1)该同学购买甲乙两种铅笔各多少支?
(2)求该同学购买这两种铅笔共花了多少元钱?
相关试题

