【题目】如图,在平行四边形![]() 中,
中,![]() ,
, ![]() ,
,![]() ,
,![]() , 垂足为
, 垂足为![]() ,在平行四边形的边上有一点
,在平行四边形的边上有一点![]() ,且
,且![]() .将平行四边形折叠,使点
.将平行四边形折叠,使点![]() 与点
与点![]() 合,折痕所在直线与平行四边形交于点
合,折痕所在直线与平行四边形交于点![]() 、
、![]() .
.

(1)求![]() 的长;
的长;
(2)请补全图形并求折痕![]() 的长.
的长.
参考答案:
【答案】(1)![]() ;(2)补全图形见解析;折痕
;(2)补全图形见解析;折痕![]() 的长为5或
的长为5或![]() .
.
【解析】
(1)在Rt△ADE中,![]() ,
,![]() ,求得
,求得![]() ,再根据勾股定理即可求解;
,再根据勾股定理即可求解;
(2)分点O在AB和AD两类讨论,当点![]() 在
在![]() 上时,可得
上时,可得![]() 是等边三角形.求得
是等边三角形.求得![]() ;点点O在AD上时,过点
;点点O在AD上时,过点![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,
,
垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,
,![]() .求出
.求出![]() ,
,![]() ,
,![]() ,
,![]() 根据折叠性质,结合勾股定理,求出
根据折叠性质,结合勾股定理,求出![]() ,进而求出
,进而求出![]() ,利用面积法即可求得
,利用面积法即可求得![]() .
.
(1)∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)如图1所示,当点![]() 在
在![]() 上时,
上时,
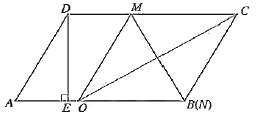
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,![]() .
.
∴![]() .
.
∵将平行四边形折叠,使点![]() 与点
与点![]() 重合,
重合,
∴折痕![]() 垂直平分
垂直平分![]() ,即
,即![]() ,
,
![]() .
.
∵折痕![]() 与平行四边形
与平行四边形![]() 的边
的边![]() 交于点
交于点![]() ,
,
∴点![]() 与点
与点![]() 重合.
重合.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() 是等边三角形.
是等边三角形.
∴![]() .
.
如图2所示,当点![]() 在
在![]() 上时,
上时,
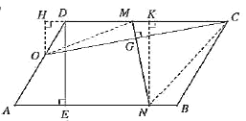
过点![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,
,
垂足分别为![]() 、
、![]() , 连接
, 连接![]() ,
,![]() .
.
∵四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
∴![]() ,
,![]() ,
,![]()
∴![]() ,
,![]()
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() ,
,
![]() .
.
∴在![]() 中,
中,![]() ,
,
由折叠可知,![]() ,
,![]() .
.
∴在![]() 中,
中,![]() ,
,
即![]() .
.
∴![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
∴四边形![]() 为矩形.
为矩形.
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() .
.
综上所述,折痕![]() 的长为5或
的长为5或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,AB=AC=8,∠BAC=30°,将△ABC绕点A旋转,使点B落在原△ABC的点C处,此时点C落在点D处,延长线段AD,交原△ABC的边BC的延长线于点E,那么线段DE的长等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
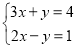 ;
;(2)
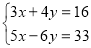 ;
;(3)
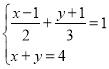 .
. -
科目: 来源: 题型:
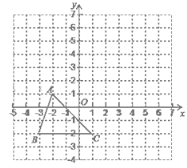
查看答案和解析>>【题目】已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′.
(1)写出A′、B′、C′的坐标;
(2)求出△ABC的面积;
(3)点P在y轴上,且△BCP是△ABC的面积的2倍,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】整式运算
(1)(x4)3÷(﹣x2)2+(﹣x2)3x2
(2)(x+3)(x﹣5)+2x(3x﹣1)
(3)(2b﹣a)(2a+b)﹣2(3a﹣2b)2
(4)
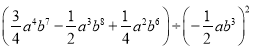 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
若一个整数能表示成a2+b2(a、b是整数)的形式,则称这个数为“平和数”,例如5是“平和数”,因为5=22+1,再如,M=x2+2xy+2y2=(x+y)2+y2(x,y是整数),我们称M也是“平和数”.
(1)请你写一个小于5的“平和数”,并判断34是否为“平和数”.
(2)已知S=x2+9y2+6x﹣6y+k(x,y是整数,k是常数,要使S为“平和数”,试求出符合条件的一个k值,并说明理由.
(3)如果数m,n都是“平和数”,试说明
 也是“平和数”.
也是“平和数”. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=
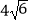 ,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为 .
,AD=10.连接BD,∠DBC的角平分线BE交DC于点E,现把△BCE绕点B逆时针旋转,记旋转后的△BCE为△BC′E′.当射线BE′和射线BC′都与线段AD相交时,设交点分别为F,G.若△BFD为等腰三角形,则线段DG长为 .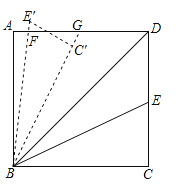
相关试题

