【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.易证:CE=CF.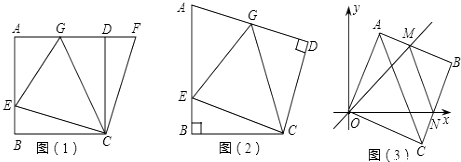
(1)在图1中,若G在AD上,且∠GCE=45°.试猜想GE,BE,GD三线段之间的数量关系,并证明你的结论.
(2)运用(1)中解答所积累的经验和知识,完成下面两题:
①如图2,在四边形ABCD中∠B=∠D=90°,BC=CD,点E,点G分别是AB边,AD边上的动点.若∠BCD=α,∠ECG=β,试探索当α和β满足什么关系时,图1中GE,BE,GD三线段之间的关系仍然成立,并说明理由.
②在平面直角坐标中,边长为1的正方形OABC的两顶点A,C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图3).设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?若不变,请直接写出结论.
参考答案:
【答案】
(1)
解:GE=BE+GD,理由如下:
∵四边形ABCD是正方形,F是AD延长线上一点,
∴BC=DC,∠FDC=∠EBC=90°,
在△EBC和△FDC中,  ,
,
∴△EBC≌△FDC(SAS),
∴∠DCF=∠BCE,CE=CF,
∵∠GCE=45°,
∴∠BCE+∠DCG=90°﹣45°=45°,
∴∠DCG+∠DCF=45°,
∴∠ECG=∠FCG,
在△ECG和△FCG中,  ,
,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∴GE=BE+GD
(2)
解:①α=2β时,GE=BE+GD;理由如下:
延长AD到F点,使DF=BE,连接CF,如图(2)所示:

∵∠B=∠D=90°,
∴∠B=∠FDC=90°,
在△EBC和△FDC中,  ,
,
∴△EBC≌△FDC(SAS),
∴∠DCF=∠BCE,CE=CF,
∴∠BCE+∠DCG=∠GCF,
当α=2β时,∠ECG=∠FCG,
在△ECG和△FCG中,  ,
,
∴△ECG≌△FCG(SAS),
∴EG=GF,
∴GE=BE+GD;
②在旋转正方形OABC的过程中,P值无变化;
延长BA交y轴于E点,如图(3)所示:

则∠AOE=45°﹣∠AOM,∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°﹣90°=90°=∠OCN.
在△OAE和△OCN中, 
∴△OAE≌△OCN(ASA).
∴OE=ON,AE=CN.
在△OME和△OMN中,  .
.
∴△OME≌△OMN(SAS).
∴MN=ME=AM+AE.
∴MN=AM+CN,
∴P=MN+BN+BM=AM+CN+BN+BM=AB+BC=2.
∴在旋转正方形OABC的过程中,P值无变化.
【解析】(1)由SAS证得△EBC≌△FDC,再由SAS证得△ECG≌△FCG,可得到EG=FG,即可得出结果;(2)①延长AD到F点,使DF=BE,连接CF,可证△EBC≌△FDC,结合条件可证得△ECG≌△FCG,故EG=GF,可得出结论;②延长BA交y轴于E点,可证得△OAE≌△OCN,进一步可证得△OME≌△OMN,可求得MN=AM+AE
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+4x+4+m的图像与y轴交于点C,点B与点C的纵坐标相同,一次函数y=kx+b的与二次函数交于A、B两点,且A点坐标为(-1,0).
(1)求二次函数与一次函数的解析式;
(2)若抛物线对称轴上存在一点P,直线PC将△ABC分成面积为1:2两部分,求P点坐标。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的三边长都是整数,最长边长为8,则满足上述条件的互不全等的三角形的个数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 相等的角是对顶角B. 同位角相等
C. 两直线平行,同旁内角相等D. 垂线段最短
-
科目: 来源: 题型:
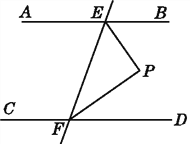
查看答案和解析>>【题目】如图,已知AB∥CD,直线EF分别交AB,CD于点E,F,EP平分∠BEF,FP平分∠DFE.试说明:△PEF是直角三角形.
-
科目: 来源: 题型:
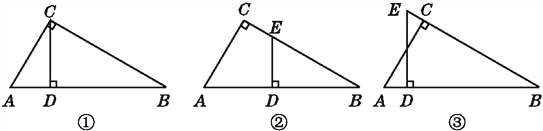
查看答案和解析>>【题目】(1)如图①,CD是直角三角形ABC斜边AB上的高,图中有与∠A相等的角吗?为什么?
(2)如图②,把图①中的CD平移到ED处,图中还有与∠A相等的角吗?为什么?
(3)如图③,把图①中的CD平移到ED处,交BC的延长线于点E,图中还有与∠A相等的角吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾天气影响着我国北方中东部地区,给人们的健康带来严重的危害.为了让人们对雾霾有所了解.摄影师张超通过显微镜,将空气中细小的霾颗粒放大1000倍,发现这些霾颗粒平均直径为10微米20微米,其中20微米(1米=1000000微米)用科学记数法可表示为( )
A.2×105米
B.0.2×10﹣4米
C.2×10﹣5米
D.2×10﹣4米
相关试题

