【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.
![]()
![]() 若
若![]() ,求线段MN的长;
,求线段MN的长;
![]() 若C为线段AB上任一点,满足
若C为线段AB上任一点,满足![]() ,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
,其它条件不变,你能猜想MN的长度吗?并说明理由,你能用一句简洁的话描述你发现的结论吗?
![]() 若C在线段AB的延长线上,且满足
若C在线段AB的延长线上,且满足![]() cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?请画出图形,写出你的结论,并说明理由.
参考答案:
【答案】(1)MN=7cm;(2)MN=![]() a;结论:当C为线段AB上一点,且M,N分别是AC,BC的中点,则有MN=
a;结论:当C为线段AB上一点,且M,N分别是AC,BC的中点,则有MN=![]() AB;(3)MN=
AB;(3)MN=![]() b.
b.
【解析】
(1)由中点的定义可得MC、CN长,根据线段的和差关系即可得答案;(2)根据中点定义可得MC=![]() AC,CN=
AC,CN=![]() BC,利用MN=MC+CN,
BC,利用MN=MC+CN,![]() ,即可得结论,总结描述即可;(3)点在AB的延长线上时,根据M、N分别为AC、BC的中点,即可求出MN的长度.
,即可得结论,总结描述即可;(3)点在AB的延长线上时,根据M、N分别为AC、BC的中点,即可求出MN的长度.
(1)∵点M、N分别是AC、BC的中点,AC=8,CB=6,
∴MC=![]() AC=4,CN=
AC=4,CN=![]() BC=3,
BC=3,
∴MN=MC+CN=7cm.
(2)∵点M、N分别是AC、BC的中点,
∴MC=![]() AC,CN=
AC,CN=![]() BC,
BC,
∵AC+BC=AB=a,
∴MN=MC+CN=![]() (AC+BC)=
(AC+BC)=![]() a.
a.
综上可得结论:当C为线段AB上一点,且M,N分别是AC,BC的中点,则有MN=![]() AB.
AB.
(3)如图:当点C在线段AB的延长线时,则AC>BC,
∵M是AC的中点,
∴CM=![]() AC,
AC,
∵点N是BC的中点,
∴CN=![]() BC,
BC,
∴MN=CM-CN=![]() (AC-BC)=
(AC-BC)=![]() b.
b.
![]()
-
科目: 来源: 题型:
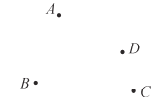
查看答案和解析>>【题目】读句画图:如图所示,A,B,C,D在同一平面内.
(1)过点A和点D画直线;
(2)画射线CD;
(3)连接AB;
(4)连接BC,并反向延长BC.
(5)已知AB=9,直线AB上有一点F,并且BF=3,则AF=_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:
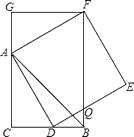
①AC=FG; ②S△FAB:S四边形CBFG=1:2;
③∠ABC=∠ABF; ④AD2=FQAC,
其中正确的结论的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
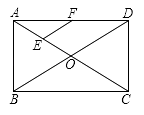
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.
-
科目: 来源: 题型:
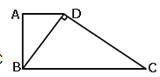
查看答案和解析>>【题目】如图,在△ABC中,点D在AB上,在下列四个条件中:①∠ACD=∠B;②∠ADC=∠ACB;③AC2=ADAB;④ABCD=ADCB,能满足△ADC与△ACB相似的条件是( )

A.①、②、③ B.①、③、④ C.②、③、④ D.①、②、④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,∠BAD=90°,对角线BD⊥DC, 如果AD=4,BC=9,则BD的长=___________ 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明将两块完全相同的直角三角形纸片的直角顶点C叠放在一起,若保持△BCD不动,将△ACE绕直角顶点C旋转.
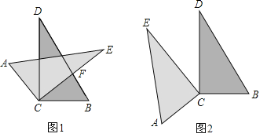
(1)如图1,如果CD平分∠ACE,那么CE是否平分∠BCD?答:______(填写“是”或“否”);
(2)如图1,若∠DCE=35,则∠ACB=______;若∠ACB=140,则∠DCE=______;
(3)当△ACE绕直角顶点C旋转到如图1的位置时,猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)当△ACE绕直角顶点C旋转到如图2的位置时,上述关系是否依然成立,请说明理由;
相关试题

