【题目】如图,已知四边形ABCD为正方形,AB=2 ![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.
参考答案:
【答案】
(1)
解:如图,作EM⊥BC,EN⊥CD
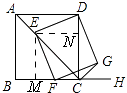
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
在△DEM和△FEM中,
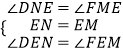 ,
,
∴△DEM≌△FEM,
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)
解:CE+CG的值是定值,定值为4,
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
∴△ADE≌△CDG,
∴AE=CG.
∴CE+CG=CE+AE=AC= ![]() AB=
AB= ![]() ×2
×2 ![]() =4,
=4,
(3)
解:如图,
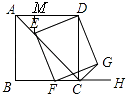
∵正方形ABCD中,AB=2 ![]() ,
,
∴AC=4,
过点E作EM⊥AD,
∴∠DAE=45°,
∵AE=x,
∴AM=EM= ![]() x,
x,
在Rt△DME中,DM=AD﹣AM=2 ![]() ﹣
﹣ ![]() x,EM=
x,EM= ![]() x,
x,
根据勾股定理得,DE2=DM2+EM2=(2 ![]() ﹣
﹣ ![]() x)2+(
x)2+( ![]() x)2=x2﹣4x+8,
x)2=x2﹣4x+8,
∵四边形DEFG为正方形,
∴S=S正方形DEFG=DE2=x2﹣4x+8.
【解析】(1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEM≌△FEM,则有DE=EF即可;(2)同(1)的方法判断出△ADE≌△CDG得到CG=AE,即:CE+CG=CE+AE=AC=4;(3)由正方形的性质得到∠DAE=45°,表示出AM=EM,再表示出DM,再用勾股定理求出DE2 .
【考点精析】关于本题考查的正方形的判定方法,需要了解先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将△ABC沿着某一方向平移一定的距离得到△MNL,则下列结论中正确的有( )
①AM∥BN;②AM=BN;③BC=ML;④∠ACB=∠MNL。
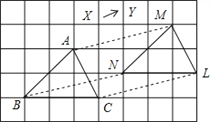
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在等边三角形ABC中,BC边上的高AD=10,E是AD上一点,现有一动点P沿着折线A-E-C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A到C的运动过程中至少需_______秒.
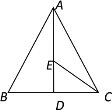
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.
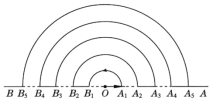
A. 5050π B. 5050π+101 C. 5055π D. 5055π+101
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC=
 .
.(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)在(2)的条件下,当点A运动到什么位置时,△AOB的面积是
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是____cm2.
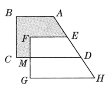
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
相关试题

