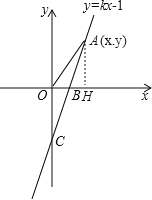
【题目】如图,直线y=kx-1与x轴、y轴分别交于B、C两点,OB:OC=![]() .
.
(1)求B点的坐标和k的值.
(2)若点A(x,y)是第一象限内的直线y=kx-1上的一个动点,当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3)在(2)的条件下,当点A运动到什么位置时,△AOB的面积是![]() .
.

参考答案:
【答案】(1)B(![]() ,0),OB=
,0),OB=![]() (2)S=
(2)S= ![]()
![]() ,(x>
,(x>![]() ) (3)A(
) (3)A(![]() ,
,![]() )
)
【解析】
(1)可先求出OC长,并用k的代数式表示点B的坐标及OB的长,然后在△BOC中运用三角函数可求出∠OCB的度数,再运用三角函数就可解决问题.
(2)过点A作AH⊥x轴于H,由于点A在直线y=kx-1上,因此可用x的代数式表示y,进而可得到S与x的函数关系式.
(3)把S=![]() 代入(2)中的解析式就可得到点A的横坐标,进而可得到点A的纵坐标.
代入(2)中的解析式就可得到点A的横坐标,进而可得到点A的纵坐标.
(1)在Rt△BOC中,
∵![]() =0,
=0,
∴k![]() 1=0.
1=0.
∴![]() =
=![]() .
.
∴点B的坐标为(![]() ,0),OB=
,0),OB=![]() .
.
∵![]() =0,∴
=0,∴![]() =01=1.
=01=1.
∴![]() =1.∴OC=1.
=1.∴OC=1.
∵sin∠OCB=![]() ,
,
∴∠OCB=30°.
∴tan∠OCB=![]() .
.
∴OB=![]() OC.
OC.
∴![]() =
=![]() ×1.
×1.
∴k=![]() .
.
∴B点坐标为(![]() ,0),k的值为
,0),k的值为![]() .
.
(2)过点A作AH⊥x轴于H,如图.
则有AH=y=![]() x1.x>
x1.x>![]() .
.
∴S=![]() OBAH=
OBAH=![]() ×
×![]() ×(
×(![]() x1)=
x1)= ![]()
![]() ,(x>
,(x>![]() ).
).
(3)当S△AOB=![]() 时,
时, ![]()
![]() =
=![]() .
.
解得;x=![]() .
.
∴y=![]() x 1=
x 1=![]() ×
×![]() 1=
1=![]() .
.
∴点A的坐标为(![]() ,
,![]() ).
).
∴当点A运动到点(![]() ,
,![]() )的位置时,△AOB的面积是
)的位置时,△AOB的面积是![]() .
.
-
科目: 来源: 题型:
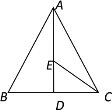
查看答案和解析>>【题目】如图所示,在等边三角形ABC中,BC边上的高AD=10,E是AD上一点,现有一动点P沿着折线A-E-C运动,在AE上的速度是4单位/秒,在CE上的速度是2单位/秒,则点P从A到C的运动过程中至少需_______秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O在直线AB上,点A1,A2,A3,…在射线OA上,点B1,B2,B3,…在射线OB上,图中的每一个实线段和虚线段的长均为1个单位长度.一个动点M从O点出发,按如图所示的箭头方向沿着实线段和以O为圆心的半圆匀速运动,速度为每秒1个单位长度.按此规律,则动点M到达A101点处所需时间为( )秒.
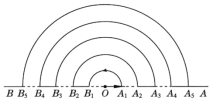
A. 5050π B. 5050π+101 C. 5055π D. 5055π+101
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD为正方形,AB=2
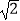 ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;
(3)设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式. -
科目: 来源: 题型:
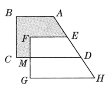
查看答案和解析>>【题目】如图,把直角梯形ABCD沿AD方向平移到梯形EFGH的位置,HG=24cm,MG=8cm,MC=6cm,则阴影部分的面积是____cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂计划生产A,B两种产品共10件,其生产成本和利润如下表:
A种产品
B种产品
成本(万元/件)
2
5
利润(万元/件)
1
3
(1)若工厂计划获利14万元,问A,B两种产品应分别生产多少件?
(2)若工厂计划投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?
(3)在(2)的条件下,哪种生产方案获利最大?并求出最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB、BC、AC三边的长分别为
 ,
,  ,
,  ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为
 ,
,  ,
,  ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .(3)在△ABC中,AB=2
 ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
相关试题

