【题目】已知:正方形纸片ABCD的边长为4,将该正方形纸片沿EF折叠(E,F分别在AB,CD边上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P.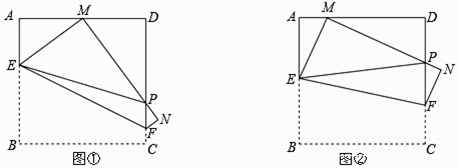
(1)如图①,连接PE,若M是AD边的中点.
①写出图中与△PMD相似的三角形.
②求△PMD的周长.
(2)如图②,随着落点M在AD边上移动(点M不与A、D重合),△PDM的周长是否发生变化?请说明你的理由.
参考答案:
【答案】
(1)
解:①依据翻折的性质可知∠EMP=∠B=90°,∠C=∠N=90°
∴∠AME+∠PMD=90°.
又∵∠AME+∠AEM=90°,
∴∠AEM=∠PMD.
又∵∠A=∠D,
∴△AME∽△DPM.
∵∠MPD=∠FPN,∠D=∠N=90°
∴△MPD∽△FPN.
∵△AME∽△DPM,
∴ ![]() .
.
又∵AM=MD,
∴ ![]() .
.
又∵∠EMP=∠D=90°,
∴△EMP∽△MDP.
所以有:△AME∽△DPM,△AME∽△DPM,△EMP∽△MDP.
②∵四边形ABCD是正方形,
∴AD=AB=4.
∵点M是AD边中点,
∴AM=DM=2.
由折叠的性质得:ME=BE,
∴△MEA的周长为6.
在Rt△MEA中,设AE=x,则ME=4﹣x.
∴x2+22=(4﹣x)2,解得:x= ![]() .
.
∵△PMD∽△MEA,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() .
.
∴△PMD的周长为8
(2)
解:△PMD的周长不变.
设AM=m,AE=n,则DM=4﹣m,EM=4﹣n,△AEM的周长=4+m.
在Rt△AME中,依据勾股定理可知:m2+n2=(4﹣n)2,即8n=16﹣m2.
∵△PMD∽△MEA,
∴ ![]() =
= ![]() .
.
∴△PMD的周长= ![]() =
= ![]() =
= ![]() =8
=8
【解析】(1)①依据两组角对应相等的三角形相似可证明△AEM∽△DMP,△PFN∽△PMD,然后依据两组边对应成比例且夹角相等的两个三角形相似证明△EMP∽△MDP即可;②设AE=x,则EM=4﹣x,在Rt△AEM中,依据勾股定理可求得x的值,然后可求得△AEM的周长,然后依据相似三角形的周长比等于相似比求解即可;(2)设AM=m,AE=n,则DM=4﹣m,EM=4﹣n.在Rt△AEM中,依据勾股定理和完全平方公式可得到8n=16﹣m2 , 然后可△PMD∽△MEA可求得△PMD的周长.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)和相似三角形的应用的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B是平面上的两定点,在平面上找一点C,使△ABC为等腰直角三角形,且点C为直角顶点,这样的点C有几个?请用尺规作图确定点C的位置,保留作图迹并说明理由

-
科目: 来源: 题型:
查看答案和解析>>【题目】在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别做出了一次函数l1和l2的图像,l1与坐标轴的交点分别为点A、点B,l1与l2的交点为点C,但被同桌小英不小心用墨水给部分污染了,我们一起来探讨
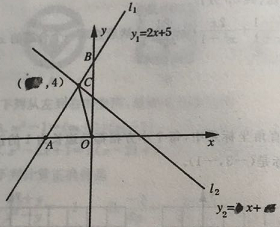
(1)写出点A、点C的坐标:A(①,0);C(②,4);
(2)求△BOC的面积:S△BOC=③
(3)直接写出不等式2x+5<·x+·的解集并回答下面问题
在解决问题(3)时,小明和小英各抒己见.小明:“l2的表达式中已经看不清楚了,并且只知道l2上一个点C的坐标,求不出该直线的表达式,所以无法求出该不等式的解集”小英说:“不用求出l2的表达式就可以得出该不等式的解集.”你同意谁的说法?并说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数分别填在相应的集合里:
 5,
5, 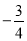 ,0,
,0,  3.14,
3.14, 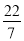 ,2016,1.99,
,2016,1.99,  (
( 6),
6), 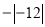
(1)正数集合:{ };
(2)负数集合:{ };
(3)整数集合;{ };
(4)分数集合:{ }.
-
科目: 来源: 题型:
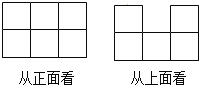
查看答案和解析>>【题目】用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?
(1)它最多需要多少个小立方体?它最少需要多少个小立方体?
(2)请你画出这两种情况下的从左面看到的形状图.
-
科目: 来源: 题型:
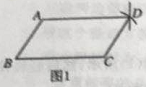
查看答案和解析>>【题目】盈盈同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证
已知:如图1,在四边形ABCD中,BC=AD,________________________
求证:________________________
(1)填空,补全已知和求证
(2)按盈盈的想法写出证明
(3)用文字叙述所证命题的逆命题为________________________

-
科目: 来源: 题型:
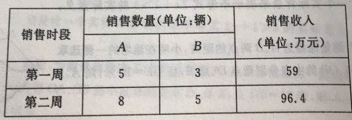
查看答案和解析>>【题目】2017年12月29日郑州市人民政府通告:为减少机动车污染物排放,持续改善我市空气质量,从2018年1月1日起,每周工作日的7时至21时郑州市东三环、南三环、西三环、北三环以内区域的所有道路限行按机动车号牌(含临时号牌和外地号牌)最后一位阿拉伯数字(尾数为字母的以末尾数字为准),工作日每天限行2个号,即:号码最后一位阿拉伯数字为1和6的机动车周一限行,2和7的机动车周二限行,3和8的机动车周三限4和9的机动车周四限行,5和0的机动车周五限行,因法定节假日放假、调休而调整为上班的周六、周日按对应调体的工作日限行但通告中还规定,悬挂新能源专用牌的新能源汽车不受限制.限行通告发布后,新能源汽车成为畅销车型,某4S店销售每辆进价分别为5万元、9万元的A、B两种型号的新能源汽车,下表是近两周的销售情况:
(1)求A、B两种型号的新能源汽车的销售单价;(共
(2)若4S店准备用不超过200万元的金额采购这两种型号的新能源汽车共30辆,求B型号的新能源汽车最多能采购多少辆?
(进价、售价均保持不变,利润=销售收入一进货成本)
(3在(2)的条件下,4S销售完这230辆新能源汽车时45店的最大利润是多少?并写
相关试题

