【题目】如图,在△ABC中,∠A=36°,AB=AC,BD是△ABC的角平分线.若在边AB上截取BE=BC,连接DE,则图中等腰三角形共有( ) 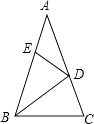
A.2个
B.3个
C.4个
D.5个
参考答案:
【答案】D
【解析】解:∵AB=AC, ∴△ABC是等腰三角形;
∵AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBC= ![]() ∠ABC=36°,
∠ABC=36°,
∴∠A=∠ABD=36°,
∴BD=AD,
∴△ABD是等腰三角形;
在△BCD中,∵∠BDC=180°﹣∠DBC﹣∠C=180°﹣36°﹣72°=72°,
∴∠C=∠BDC=72°,
∴BD=BC,
∴△BCD是等腰三角形;
∵BE=BC,
∴BD=BE,
∴△BDE是等腰三角形;
∴∠BED=(180°﹣36°)÷2=72°,
∴∠ADE=∠BED﹣∠A=72°﹣36°=36°,
∴∠A=∠ADE,
∴DE=AE,
∴△ADE是等腰三角形;
∴图中的等腰三角形有5个.
故选D.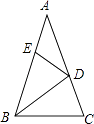
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车从A地出发沿同一路线驶向B地,甲车先出发匀速驶向B地.40分钟后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时,由于满载货物,为了行驶安全,速度减少了50千米/时,结果与甲车同时到达B地.甲乙两车距A地的路程y(千米)与乙车行驶时间x(小时)之间的函数图象如图所示.
请结合图象信息解答下列问题:
(1)直接写出a的值,并求甲车的速度;
(2)求图中线段EF所表示的y与x的函数关系式,并直接写出自变量x的取值范围;
(3)乙车出发多少小时与甲车相距15千米?直接写出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2
 =(1+
=(1+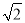 )2.善于思考的小明进行了以下探索:
)2.善于思考的小明进行了以下探索:设a+b
 =(m+n
=(m+n )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b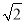 =m2+2n2+2mn
=m2+2n2+2mn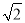 .
.∴a=m2+2n2,b=2mn.这样小明就找到了一种把类似a+b
 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b
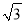 =
=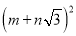 ,用含m、n的式子分别表示a、b,得:a=__,b=__;
,用含m、n的式子分别表示a、b,得:a=__,b=__;(2)利用所探索的结论,找一组正整数a、b、m、n填空:__+__
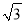 =(___)+__
=(___)+__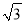 )2;
)2;(3)若a+4
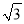 =
=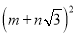 ,且a、m、n均为正整数,求a的值?
,且a、m、n均为正整数,求a的值? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是
A. 某种彩票中奖的概率是
 ,买1000张该种彩票一定会中奖
,买1000张该种彩票一定会中奖B. 了解一批电视机的使用寿命适合用抽样调查
C. 若甲组数据的标准差S甲=0.31,乙组数据的标准差S乙=0.25,则乙组数据比甲组数据稳定
D. 在一个装有白球和绿球的袋中摸球,摸出黑球是不可能事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法正确的是( )
A. 各边都相等的多边形是正多边形
B. 到线段两个端点距离相等的点在线段的垂直平分线上
C. 角的平分线就是角的对称轴
D. 形状相同的两个三角形是全等三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】在下列多项式中,有相同因式的是( )
①x2+5x+6 ; ②x2+4x+3; ③x2+6x+8 ; ④x2﹣2x﹣15 ; ⑤x2﹣x﹣20.
A.只有①⑤
B.只有②④
C.只有③⑤
D.以上答案均不对
相关试题

