【题目】请阅读某同学解下面分式方程的具体过程.
解方程![]()
解:![]() ①
①
![]() ②
②
![]() ③
③
∴![]() ④
④
∴![]() .
.
把![]() 代入原方程检验知
代入原方程检验知![]() 是原方程的解.
是原方程的解.
请你回答:
(1)得到①式的做法是 ;
得到②式的具体做法是 ;
得到③式的具体做法是 ;
得到④式的根据是 .
(2)上述解答正确吗?如果不正确,从哪一步开始出现错误?答: .错误的原因是 (若第一格回答“正确”的,此空不填).
参考答案:
【答案】(1)得到①式的做法是移项;得到②式的具体做法是方程两边分别通分;得到③式的具体做法是方程两边同除以(-2x+10);得到④式的根据是分式值相等,分子相等且不为0,则分母相等.
(2)有错误.从第③步出现错误,错误的原因是方程两边同时除以了(-2x+10),而-2x+10可能为零,当-2x+10为零时,方程两边同时除以了0,不符合等式的性质.
【解析】
本题考查解分式方程的能力,应先根据方程特点,进行整理然后去分母,将分式方程转化为整式方程求解.
解:(1)得到①式的做法是移项;
得到②式的具体做法是方程两边分别通分;
得到③式的具体做法是方程两边同除以(-2x+10);
得到④式的根据是分式值相等,分子相等且不为0,则分母相等;
(2)有错误.从第③步出现错误,错误的原因是方程两边同时除以了(-2x+10),而-2x+10可能为零,当-2x+10为零时,方程两边同时除以了0,不符合等式的性质;
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)

(2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
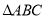 是边长
是边长 的等边三角形,动点
的等边三角形,动点 、
、 同时从
同时从 、
、 两点出发,分别在
两点出发,分别在 、
、 边上匀速移动,它们的速度分别为
边上匀速移动,它们的速度分别为 ,
, ,当点
,当点 到达点
到达点 时,P、Q两点停止运动,设点
时,P、Q两点停止运动,设点 的运动时间为
的运动时间为 ,则当
,则当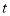 =_____
=_____ 时,
时, 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )

A. π-4 B.
 π-1 C. π-2 D.
π-1 C. π-2 D.  -2
-2【答案】C
【解析】试题解析:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴△OBC的BC边上的高为:
 OB=
OB= ,
,∴BC=2

∴S阴影=S扇形OBC﹣S△OBC=
 .
.故选C.
【题型】单选题
【结束】
10【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形,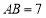 ,点
,点 是边
是边 上一点,点
上一点,点 是线段
是线段 上点,连接
上点,连接 、
、 .当
.当 ,
, 时,
时, ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱能装的文具是A型包装箱1.5倍,单独使用B型包装箱比单独使用A型包装箱可少用12个。那么A、B型包装箱每个分别可以装多少件文具?
-
科目: 来源: 题型:
查看答案和解析>>【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
【答案】A.
【解析】
试题分析:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似,
设树高x米,则
 ,即
,即 ,解得,x=8. 故选A.
,解得,x=8. 故选A.考点:相似三角形的应用.
【题型】单选题
【结束】
11【题目】已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
相关试题

