【题目】某单位向一所希望小学赠送1080件文具,现用A、B两种不同的包装箱进行包装,已知每个B型包装箱能装的文具是A型包装箱1.5倍,单独使用B型包装箱比单独使用A型包装箱可少用12个。那么A、B型包装箱每个分别可以装多少件文具?
参考答案:
【答案】每个A型包装箱可以装文具30件,每个B型包装箱可以装文具45件.
【解析】
设每个A型包装箱可以装文具x件,则每个B型包装箱可以装文具1.5x件,根据装1080件文具单独使用B型包装箱比单独使用A型包装箱可少用12个,即可得出关于x的分式方程,解之经检验后即可得出结论.
解:设每个A型包装箱可以装文具x件,则每个B型包装箱可以装文具1.5 x件,根据题意得
![]()
解得:x=30.
经检验,x=30是原方程的解,且符合题意.
当x=30,1.5 x =45
答:每个A型包装箱可以装文具30件,每个B型包装箱可以装文具45件.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )

A. π-4 B.
 π-1 C. π-2 D.
π-1 C. π-2 D.  -2
-2【答案】C
【解析】试题解析:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴△OBC的BC边上的高为:
 OB=
OB= ,
,∴BC=2

∴S阴影=S扇形OBC﹣S△OBC=
 .
.故选C.
【题型】单选题
【结束】
10【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读某同学解下面分式方程的具体过程.
解方程

解:
 ①
① ②
② ③
③ ∴
 ④
④∴
 .
.把
 代入原方程检验知
代入原方程检验知 是原方程的解.
是原方程的解.请你回答:
(1)得到①式的做法是 ;
得到②式的具体做法是 ;
得到③式的具体做法是 ;
得到④式的根据是 .
(2)上述解答正确吗?如果不正确,从哪一步开始出现错误?答: .错误的原因是 (若第一格回答“正确”的,此空不填).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形,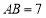 ,点
,点 是边
是边 上一点,点
上一点,点 是线段
是线段 上点,连接
上点,连接 、
、 .当
.当 ,
, 时,
时, ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
【答案】A.
【解析】
试题分析:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似,
设树高x米,则
 ,即
,即 ,解得,x=8. 故选A.
,解得,x=8. 故选A.考点:相似三角形的应用.
【题型】单选题
【结束】
11【题目】已知圆锥的底面半径为1cm,母线长为3cm,则其全面积为________cm2 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣
 x2
x2【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣
 ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣ x2.
x2.考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 的三个顶点坐标为
的三个顶点坐标为 ,
, ,
, .
.
(1)将
 绕坐标原点
绕坐标原点 逆时针旋转
逆时针旋转 ,画出对应图形
,画出对应图形 ,
,(2)并写出点
 的对应点
的对应点 的坐标______;点
的坐标______;点 关于原点对称的对应点
关于原点对称的对应点 坐标_______;
坐标_______;(3)请直接写出:以
 、
、 、
、 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点 的坐标______.
的坐标______.
相关试题

