【题目】如图,![]() 是边长
是边长![]() 的等边三角形,动点
的等边三角形,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点出发,分别在
两点出发,分别在![]() 、
、![]() 边上匀速移动,它们的速度分别为
边上匀速移动,它们的速度分别为![]() ,
,![]() ,当点
,当点![]() 到达点
到达点![]() 时,P、Q两点停止运动,设点
时,P、Q两点停止运动,设点![]() 的运动时间为
的运动时间为![]() ,则当
,则当![]() =_____
=_____![]() 时,
时,![]() 为直角三角形.
为直角三角形.

参考答案:
【答案】1.5或2.4
【解析】
分∠PQB=90°、∠QPB=90°两种情况,根据直角三角形的性质列式计算,得到答案.
解:由题意得,BQ=t,AP=2t,
则BP=6-2t,
当∠PQB=90°时,∠B=60°,
∴∠BPQ=30°,
∴BQ=![]() BP,即t=
BP,即t=![]() (6-2t),
(6-2t),
解得,t=1.5,
当∠QPB=90°时,∠B=60°,
∴∠BQP=30°,
∴BP=![]() BQ,即t=2(6-2t),
BQ,即t=2(6-2t),
解得,t=2.4,
综上所述,当t=1.5或2.4s时,△PBQ为直角三角形,
故答案为:1.5或2.4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人两次同时在一家粮店购买大米,两次大米的价格分别为每千克a元和b元(a≠b).甲每次买100千克大米,乙每次买100元大米.
(1)用含a、b的代数式表示:甲两次购买大米共需付款 元,乙两次共购买 千克大米.若甲两次购买大米的平均单价为每千克Q1元,乙两次购买大米的平均单价为每千克Q2元.则:Q1= ;Q2= .
(2)若规定谁两次购粮的平均价格低,谁购粮的方式就更合理,请你判断比较甲、乙两人的购粮方式,哪一个更合理,并说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为P(4,-4)的二次函数图象经过原点(0,0),点A在该图象上,OA交其对称轴l于点M,点M、N关于点P对称,连接AN、ON.
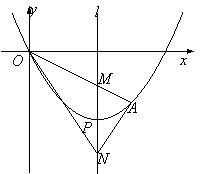
(1)求该二次函数的关系式;
(2)若点A的坐标是(6,-3),求△ANO的面积;
(3)当点A在对称轴l右侧的二次函数图象上运动时,请解答下面问题:
①证明:∠ANM=∠ONM;
②△ANO能否为直角三角形?如果能,请求出所有符合条件的点A的坐标;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程
(1)

(2)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C在⊙O上,若∠BAC=45°,OB=2,则图中阴影部分的面积为( )

A. π-4 B.
 π-1 C. π-2 D.
π-1 C. π-2 D.  -2
-2【答案】C
【解析】试题解析:∵∠BAC=45°,
∴∠BOC=90°,
∴△OBC是等腰直角三角形,
∵OB=2,
∴△OBC的BC边上的高为:
 OB=
OB= ,
,∴BC=2

∴S阴影=S扇形OBC﹣S△OBC=
 .
.故选C.
【题型】单选题
【结束】
10【题目】夏季的一天,身高为1.6m的小玲想测量一下屋前大树的高度,她沿着树影BA由B到A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m,CA=0.8m,于是得出树的高度为( )

A.8m B.6.4m C.4.8m D.10m
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读某同学解下面分式方程的具体过程.
解方程

解:
 ①
① ②
② ③
③ ∴
 ④
④∴
 .
.把
 代入原方程检验知
代入原方程检验知 是原方程的解.
是原方程的解.请你回答:
(1)得到①式的做法是 ;
得到②式的具体做法是 ;
得到③式的具体做法是 ;
得到④式的根据是 .
(2)上述解答正确吗?如果不正确,从哪一步开始出现错误?答: .错误的原因是 (若第一格回答“正确”的,此空不填).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是等边三角形,
是等边三角形,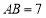 ,点
,点 是边
是边 上一点,点
上一点,点 是线段
是线段 上点,连接
上点,连接 、
、 .当
.当 ,
, 时,
时, ________.
________.
相关试题

