【题目】如图,△DAC 和△EBC 均是等边三角形,A,C,B 三点在一条直线上,AE,BD 分别与 CD、CE 交于点 M、N,AE,BD 相交于点 O.
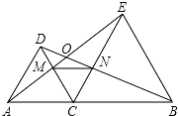
(1)求证:△ACE ≌△DCB;
(2)求∠AOD 的度数
(3)判断△CMN 的形状并说明理由。
参考答案:
【答案】(1)见详解;(2)60°;(3)见详解.
【解析】
(1)欲证三角形全等,利用全等的条件进行判定即可;因为△DAC和△ECB均为等边三角形,即有∠ACD=∠ECB=60°,再注明即可得出∠ACD=∠DCB,利用边的关系,即可得证△ACE≌△DCB;
(2)由全等三角形的性质和三角形的外角性质即可得出结果;
(3)先证△MCE≌△NCB,从而得到MC=NC,再根据有一个角是60°的等腰三角形是等边三角形可判断△CMN 的形状是等边三角形.
(1)证明:∵△DAC是等边三角形,
∴AC=DC,∠ACD=60°,
∵△BCE为等边三角形,
∴CE=CB,∠ECB=60°,
∴∠ACD=∠ECB=60°,
∴∠ACD+∠DCE=∠ECB+∠DCE,
即∠ACE=∠DCB,
在△ACE和△BCD中,
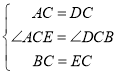 ,
,
∴△ACE≌△DCB(SAS);
(2)解:∵△ACE≌△DCB,
∴∠AEC=∠ABD.
∵∠AEC+∠BAO=∠BCE=60°
∴∠ABD +∠BAO=∠BCE=60°,
∵∠ABD +∠BAO=∠AOD,
∴∠AOD=60°.
(3)解:△CMN是等边三角形,理由如下:
∵△ACE≌△DCB,
∴∠AEC=∠ABD.
在△MCE和△NCB中,
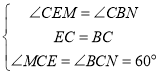
∴△MCE≌△NCB(ASA)
∴CM=CN,
∵![]()
∴△CMN是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)请画出△ABC关于y轴对称的△A′B′C′(其中A′,B′,C′分别是A,B,C的对应点,不写画法);
(2)直接写出A′,B′,C′三点的坐标:A′( ),B′( ),C′( )
(3)计算△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是小明同学解方程的过程,请仔细阅读,并解答所提出的问题.
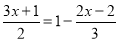
解:去分母,得
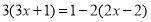 ,①
,①去括号,得
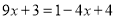 ,②
,②移项,得
 ,③
,③合并同类项,得
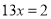 ,④
,④系数化为
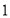 ,得
,得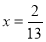 .⑤
.⑤(1)聪明的你知道小明的解答过程在________(填序号)处出现了错误,出现错误的原因是违背了__________.
A.等式的基本性质
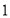 ;B.等式的基本性质
;B.等式的基本性质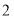 ;C.去括号法则;D加法交换律.
;C.去括号法则;D加法交换律.(2)请你写出正确的解答过程
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=
 时,求P点坐标.
时,求P点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA 交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若
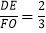 ,求证:CD=DH.
,求证:CD=DH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,某活动小组用棋子摆出了下列图形:



 ……
……第1个图形 第2个图形 第3个图形 第4个图形
(1)探索新知:
①第
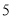 个图形需要_________枚棋子;②第
个图形需要_________枚棋子;②第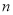 个图形需要__________枚棋子.
个图形需要__________枚棋子.(2)思维拓展:
小明说:“我要用
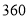 枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由.
枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE⊥AC,连结 DF 交射线 AC 于点 G
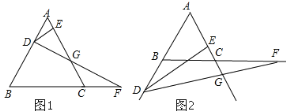
(1)当 DF⊥AB 时,求 t 的值;
(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
(3)聪明的斯扬同学通过测量发现,当点 D 在线段 AB 上时,EG 的长始终等于 AC 的一半,他想当点D 运动到图 2 的情况时,EG 的长是否发生变化?若改变,说明理由;若不变,求出 EG 的长。
相关试题

