【题目】如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE⊥AC,连结 DF 交射线 AC 于点 G
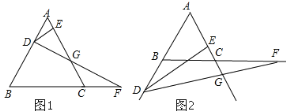
(1)当 DF⊥AB 时,求 t 的值;
(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
(3)聪明的斯扬同学通过测量发现,当点 D 在线段 AB 上时,EG 的长始终等于 AC 的一半,他想当点D 运动到图 2 的情况时,EG 的长是否发生变化?若改变,说明理由;若不变,求出 EG 的长。
参考答案:
【答案】(1)![]() ;(2)见详解;(3)不变.
;(2)见详解;(3)不变.
【解析】
(1)设AD=x,则BD=4-x,BF=4+x.当DF⊥AB时,通过解直角△BDF求得x的值,易得t的值;
(2)如图1,过点D作DH∥BC交AC于点H,构建全等三角形:△DHG≌△FCG,结合全等三角形的对应边相等的性质和图中相关线段间的和差关系求得DG=GF;
(3)过F作FH⊥AC,可证△ADE≌△CFH,得DE=FH,AC=EH,再证△GDE≌△GFH,可得EG=GH,即可解题.
解:(1)设AD=x,则BD=4-x,BF=4+x.
当DF⊥AB时,∵∠B=60°,
∴∠DFB=30°,
∴BF=2BD,即4+x=2(4-x),
解得x=![]() ,
,
故t=![]() ;
;
(2)如图1,过点D作DH∥BC交AC于点H,则∠DHG=∠FCG.
∵△ABC是等边三角形,
∴△ADH是等边三角形,
∴AD=DH.
又AD=CF,
∴DH=FC.
∵在△DHG与△FCG中,
 ,
,
∴△DHG≌△FCG(AAS),
∴DG=GF;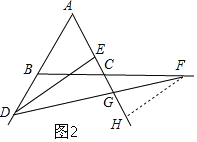
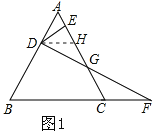
(3)如图2,过F作FH⊥AC,
在△ADE和△CFH中,
 ,
,
∴△ADE≌△CFH(AAS),
∴DE=FH,AE=CH,
∴AC=EH,
在△GDE和△GFH中,
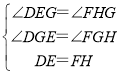 ∴△GDE≌△GFH(AAS),
∴△GDE≌△GFH(AAS),
∴EG=GH,
∴EG=![]() EH=
EH=![]() AC.
AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△DAC 和△EBC 均是等边三角形,A,C,B 三点在一条直线上,AE,BD 分别与 CD、CE 交于点 M、N,AE,BD 相交于点 O.
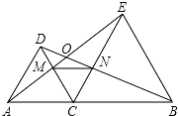
(1)求证:△ACE ≌△DCB;
(2)求∠AOD 的度数
(3)判断△CMN 的形状并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的顶点在⊙O上,BD是⊙O的直径,延长CD、BA 交于点E,连接AC、BD交于点F,作AH⊥CE,垂足为点H,已知∠ADE=∠ACB.
(1)求证:AH是⊙O的切线;
(2)若OB=4,AC=6,求sin∠ACB的值;
(3)若
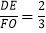 ,求证:CD=DH.
,求证:CD=DH.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,某活动小组用棋子摆出了下列图形:



 ……
……第1个图形 第2个图形 第3个图形 第4个图形
(1)探索新知:
①第
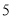 个图形需要_________枚棋子;②第
个图形需要_________枚棋子;②第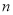 个图形需要__________枚棋子.
个图形需要__________枚棋子.(2)思维拓展:
小明说:“我要用
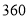 枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由.
枚棋子摆出一个符合以上规律的图形”,你认为小明能摆出吗?如果能摆出,请问摆出的是第几个图形;如果不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(4,6),点P为线段OA上一动点(与点O、A不重合),连接CP,过点P作PE⊥CP交AB于点D,且PE=PC,过点P作PF⊥OP且PF=PO(点F在第一象限),连结FD、BE、BF,设OP=t.
(1)直接写出点E的坐标(用含t的代数式表示):_____;
(2)四边形BFDE的面积记为S,当t为何值时,S有最小值,并求出最小值;
(3)△BDF能否是等腰直角三角形,若能,求出t;若不能,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )

A.4,30° B.2,60° C.1,30° D.3,60°
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论①abc<0;②(4a﹣b)(2a+b)<0;③4a﹣c<0;④若OC=OB,则(a+1)(c+1)>0,正确的为( )
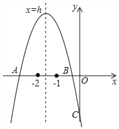
A. ①②③④ B. ①②④ C. ①③④ D. ①②③
相关试题

