搜索
【题目】在数学活动课上，某活动小组用棋子摆出了下列图形：
……
第1个图形 第2个图形 第3个图形 第4个图形
（1）探索新知：
①第
个图形需要_________枚棋子；②第
个图形需要__________枚棋子．
（2）思维拓展：
小明说：“我要用
枚棋子摆出一个符合以上规律的图形”，你认为小明能摆出吗？如果能摆出，请问摆出的是第几个图形；如果不能，请说明理由．
参考答案：
【答案】（1）①16；②
；（2）不能，见解析
【解析】
（1）①观察4个图形中的变化，得到变化规律，得到第5个图形的数量；
②根据前面发现的规律即可列式表示；
（2）将第n个图形的代数式等于360，计算出n的值，判断是否符合题意.
（1）①第1个图需要棋子枚数：1+3，
第2个图需要棋子枚数：
，
第3个图需要棋子枚数： 
，
第4个图需要棋子枚数：
，
∴第5个图需要棋子枚数： 
，
故答案为：16；
②由①得到：第n个图需要棋子枚数： ，
故答案为：；
（2）不能，
当=360时，得
，
∵n为正整数，
∴不能摆出符合以上规律的图形.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，直线y=x+2与坐标轴交于A、B两点，点A在x轴上，点B在y轴上，C点的坐标为（1，0），抛物线y=ax2+bx+c经过点A、B、C．
（1）求该抛物线的解析式；
（2）根据图象直接写出不等式ax2+（b﹣1）x+c＞2的解集；
（3）点P是抛物线上一动点，且在直线AB上方，过点P作AB的垂线段，垂足为Q点．当PQ=
时，求P点坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△DAC 和△EBC 均是等边三角形，A，C，B 三点在一条直线上，AE，BD 分别与 CD、CE 交于点 M、N，AE，BD 相交于点 O.
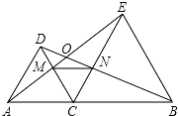
（1）求证：△ACE ≌△DCB;
（2）求∠AOD 的度数
（3）判断△CMN 的形状并说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD的顶点在⊙O上，BD是⊙O的直径，延长CD、BA 交于点E，连接AC、BD交于点F，作AH⊥CE，垂足为点H，已知∠ADE=∠ACB．
（1）求证：AH是⊙O的切线；
（2）若OB=4，AC=6，求sin∠ACB的值；
（3）若
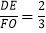，求证：CD=DH．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在边长为 4 的等边△ABC 中，点 D 从点A 开始在射线 AB 上运动，速度为 1 个单位/秒，点F 同时从 C 出发，以相同的速度沿射线 BC 方向运动，过点D 作 DE⊥AC，连结 DF 交射线 AC 于点 G
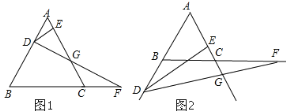
(1)当 DF⊥AB 时，求 t 的值；
(2)当点 D 在线段 AB 上运动时，是否始终有 DG=GF?若成立，请说明理由。
(3)聪明的斯扬同学通过测量发现，当点 D 在线段 AB 上时，EG 的长始终等于 AC 的一半，他想当点D 运动到图 2 的情况时，EG 的长是否发生变化?若改变，说明理由；若不变，求出 EG 的长。
-
科目： 来源： 题型：
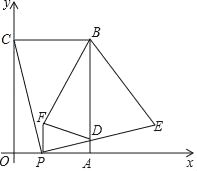
查看答案和解析>>【题目】如图，在平面直角坐标系中，矩形OABC的顶点B坐标为（4，6），点P为线段OA上一动点（与点O、A不重合），连接CP，过点P作PE⊥CP交AB于点D，且PE=PC，过点P作PF⊥OP且PF=PO（点F在第一象限），连结FD、BE、BF，设OP=t．
（1）直接写出点E的坐标（用含t的代数式表示）：_____；
（2）四边形BFDE的面积记为S，当t为何值时，S有最小值，并求出最小值；
（3）△BDF能否是等腰直角三角形，若能，求出t；若不能，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB=4，BC=6，∠B=60°，将△ABC沿射线BC的方向平移，得到△A′B′C′，再将△A′B′C′绕点A′逆时针旋转一定角度后，点B′恰好与点C重合，则平移的距离和旋转角的度数分别为（ ）
A．4，30° B．2，60° C．1，30° D．3，60°
相关试题
