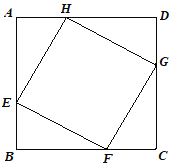
【题目】如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.则四边形EFGH面积的最小值是________cm2.
参考答案:
【答案】32
【解析】分析:根据正方形的性质结合已知可推出:△EAH≌△FBE≌△GCF≌△HDG,结合全等三角形的性质得到四边形EFGH是菱形;根据角度间关系容易得出∠HEF=90°,进而得到四边形EFGH是正方形,设AE=DH=x,则AH=8-x,在Rt△AEH中利用勾股定理可得:EH2=AE2+AH2,结合二次函数的最值解答即可.
详解:∵四边形ABCD是正方形,
∴∠BAD=∠ABC=∠BCD=∠CDA=90°,AB=BC=CD=DA.
∵AE=BF=CG=DH,
∴BE=CF=AH=DG,
∴△EAH≌△FBE≌△GCF≌△HDG,
∴EH=EF=FG=HG,∠AEH=∠BFE,
∴四边形EFGH是菱形.
∵∠BEF+∠BFE=90°,∠AEH=∠BFE,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°.
∵四边形EFGH是菱形,∠HEF=90°,
∴四边形EFGH是正方形.
正方形EFGH的面积最小,则边长EF最小.
设AE=DH=x,则AH=8-x,
∵在Rt△AEH中,EH2=AE2+AH2=x2+(8-x)2=2x2-16x+64=2(x-4)2+32,
∴四边形EFGH面积的最小值为32cm2.
-
科目: 来源: 题型:
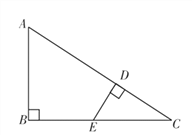
查看答案和解析>>【题目】如图,一艘军舰位于点A处,在其正南方向有一目标B,在点B的正东方向有一目标C,且AB+BC=3海里,在AC上有一艘补给船D,DC为1海里;军舰从点A出发,向AB,BC方向匀速航行,补给船同时从点D出发,沿垂直于AC方向匀速直线航行,欲将一批物品送达军舰.已知军舰的速度是补给船的2倍,军舰在由B到C的途中与补给船相遇于E处,那么相遇时补给船航行了几海里?
-
科目: 来源: 题型:
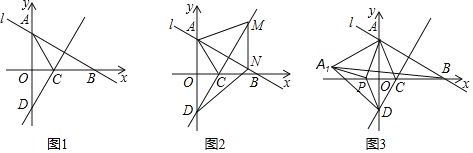
查看答案和解析>>【题目】如图1,在平面直角坐标系中,已知直线l:y
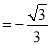 x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.
x+3交y轴于点A,x轴于点B,∠BAO的角平分线AC交x轴于点C,过点C作直线AB的垂线,交y轴于点D.(1)求直线CD的解析式;
(2)如图2,若点M为直线CD上的一个动点,过点M作MN∥y轴,交直线AB与点N,当四边形AMND为菱形时,求△ACM的面积;
(3)如图3,点P为x轴上的一个动点连接PA、PD,将△ADP沿DP翻折得到△A1DP,当以点A、A1、B为顶点的三角形是等腰三角形时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD边AB上一点(点P不与点A,B重合),连接PD,将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
(1)求∠PBE的度数;
(2)若△PFD∽△BFP,求
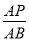 的值.
的值.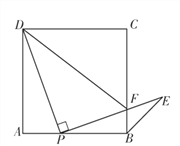
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=50°,∠DOE=35°,求∠BOD的度数;
(2)若∠AOE=160°,∠COD=40°,求∠AOB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某天昆明市交警大队的一辆警车在东西方向的街上巡视,警车从钟楼A处出发,规定向东方向为正,当天行驶纪录如下(单位:千米)
+10,-9,+7,-15,+6,-5,+4,-2
(1)最后警车是否回到钟楼A处?若没有,在钟楼A处何方,距钟楼A多远?
(2)警车行驶1千米耗油0.2升,油箱有油10升,够不够?若不够,途中还需补充多少升油?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
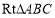 中,
中,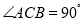 ,过点
,过点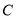 的直线
的直线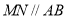 ,
,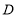 为
为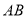 边上一点,过点
边上一点,过点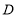 作
作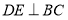 ,交直线
,交直线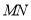 于点
于点 ,垂足为
,垂足为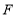 ,连接
,连接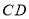 ,
, .
.(1)求证:
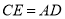 ;
;(2)当
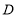 为
为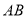 的中点时,四边形
的中点时,四边形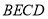 是什么特殊四边形?请说明你的理由;
是什么特殊四边形?请说明你的理由;(3)若
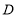 为
为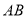 的中点,则当
的中点,则当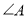 的大小满足什么条件时,四边形
的大小满足什么条件时,四边形 是正方形?请说明你的理由.
是正方形?请说明你的理由.
相关试题

