【题目】平面直角坐标系中,直线l1:![]() 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2:![]() 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.
(1)当k=1时,求点P的坐标;
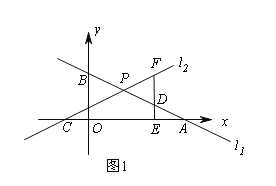
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
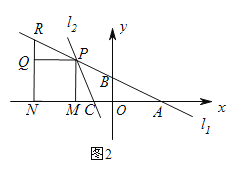
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
参考答案:
【答案】(1)P(![]() ,
,![]() );(2)
);(2)![]() ;(3)(
;(3)(![]() ,
,![]() )
)
【解析】
(1把k=1代入l2解析式,当k=1时,直线l2为y=x+2.与l1组成方程组
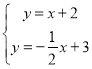 , 解这个方程组得:
, 解这个方程组得:![]() ,
,
∴P(![]() ,
,![]() );
);
(2)当y=0时,kx+2k=0 ,∵k≠0,∴x=-2,
∴C(-2,0),OC=2,当y=0时,-![]() x+3=0,∴x=6,
x+3=0,∴x=6,
∴A(6,0),OA=6 ,
过点P作PG⊥DF于点G,
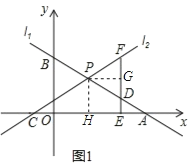
在△PDG和△ADE中,
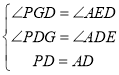
∴△PDG≌△ADE,
得DE=DG=![]() DF,
DF,
∴PD=PF,
∴∠PFD=∠PDF
∵∠PFD+∠PCA=90°,∠PDF+∠PAC=90°
∴∠PCA=∠PAC,
∴PC=PA
过点P作PH⊥CA于点H,
∴CH=![]() CA=4,
CA=4,
∴OH=2,
当x=2时,y=![]() ×2+3=2代入y=kx+2k,得k=
×2+3=2代入y=kx+2k,得k=![]() ;
;
(3)在Rt△PMC和Rt△PQR中,
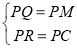
∴Rt△PMC≌Rt△PQR,
∴CM=RQ,
∴NR=NC,
设NR=NC=a,则R(a2,a),
代入y=![]() x+3,
x+3,
得![]() (a2)+3=a,解得a=8,
(a2)+3=a,解得a=8,
设P(m,n),则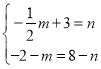
解得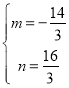
∴P(![]() ,
,![]() )
)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.

(1)在图1中,EF=___,BF=____;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的S1,S2,若m-n=2,请问S2-S1的值为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在七年级的一次“数学联欢会”上,数学老师李老师出示了10张数学答题卡,答题卡背面的图案不同:当答题卡正面是正数时,背面是一面五星红旗;当答题卡的正面是负数时,背面是一朵牡丹花。这10张答题卡如图所示:

请你指出这10张答题卡后面有几面五星红旗?有几朵牡丹花?并写出它们的卡片号码。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了弘扬二中精神,磨炼学生意志, 4 月14 日下,万州二中初2019级全体师生在学校领导和各班班主任的带领下进行了主题为“放歌平湖之家多美”的环湖拉练活动,师生们从二中初中部出发沿滨江路步行到达三峡移民纪念馆,全体师生在此进行了一个小时左右的宣传与实践活动,然后又乘车返回;设师生所用的时间为x(小时),师生们离开学校的距离为y(千米)则下列各图中,能反映y与x之间关系的图象大致是( )
A.
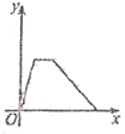 B.
B. 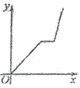 C.
C. 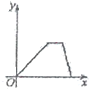 D.
D. 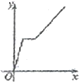
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是( )
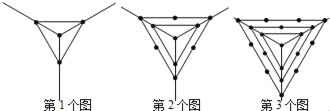
A.46B.63C.64D.73
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升
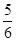 cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.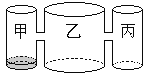
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
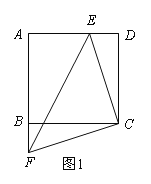

(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
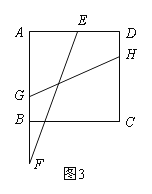
(3)如图3,点G,H分别在边AB,CD上,且GH=
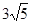 cm,连接EF,当EF与GH的夹角为45°,求t的值.
cm,连接EF,当EF与GH的夹角为45°,求t的值.
相关试题

