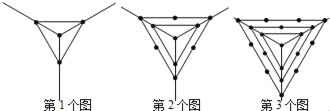
【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是( )
A.46B.63C.64D.73
参考答案:
【答案】C
【解析】
由图可知:其中第1个图中共有1+1×3=4个点,第2个图中共有1+1×3+2×3=10个点,第3个图中共有1+1×3+2×3+3×3=19个点,…,由此规律得出第n个图有1+1×3+2×3+3×3+…+3n个点.
解:第1个图中共有1+1×3=4个点,
第2个图中共有1+1×3+2×3=10个点,
第3个图中共有1+1×3+2×3+3×3=19个点,
…
第n个图有1+1×3+2×3+3×3+…+3n个点.
所以第6个图中共有点的个数是1+1×3+2×3+3×3+4×3+5×3+6×3=64.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在七年级的一次“数学联欢会”上,数学老师李老师出示了10张数学答题卡,答题卡背面的图案不同:当答题卡正面是正数时,背面是一面五星红旗;当答题卡的正面是负数时,背面是一朵牡丹花。这10张答题卡如图所示:

请你指出这10张答题卡后面有几面五星红旗?有几朵牡丹花?并写出它们的卡片号码。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了弘扬二中精神,磨炼学生意志, 4 月14 日下,万州二中初2019级全体师生在学校领导和各班班主任的带领下进行了主题为“放歌平湖之家多美”的环湖拉练活动,师生们从二中初中部出发沿滨江路步行到达三峡移民纪念馆,全体师生在此进行了一个小时左右的宣传与实践活动,然后又乘车返回;设师生所用的时间为x(小时),师生们离开学校的距离为y(千米)则下列各图中,能反映y与x之间关系的图象大致是( )
A.
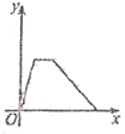 B.
B. 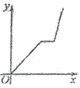 C.
C. 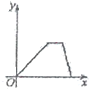 D.
D. 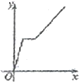
-
科目: 来源: 题型:
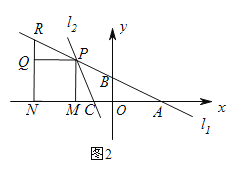
查看答案和解析>>【题目】平面直角坐标系中,直线l1:
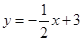 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2: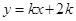 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.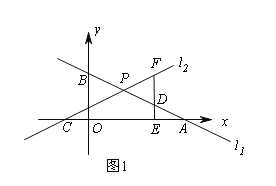
(1)当k=1时,求点P的坐标;
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升
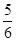 cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.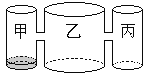
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
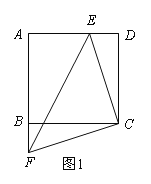

(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
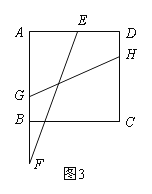
(3)如图3,点G,H分别在边AB,CD上,且GH=
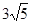 cm,连接EF,当EF与GH的夹角为45°,求t的值.
cm,连接EF,当EF与GH的夹角为45°,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.

相关试题

