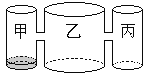
【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升![]() cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
参考答案:
【答案】![]() ,
,![]() ,
,![]()
【解析】
试题∵甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,∴甲、乙、丙三个圆柱形容器的底面积之比为1:4:1,∵每分钟同时向乙和丙注入相同量的水,注水1分钟,乙的水位上升![]() cm,∴注水1分钟,丙的水位上升
cm,∴注水1分钟,丙的水位上升![]() cm,
cm,
当甲比乙高0.5cm时,此时乙中水位高0.5cm,用时0.5÷![]() =
=![]() 分;
分;
当丙的高度到5cm时,此时用时为5÷![]() =
=![]() 分,此时乙中水高
分,此时乙中水高![]() =
=![]() <1+0.5,在这之后丙中的水流入乙中,乙每分钟水位上升
<1+0.5,在这之后丙中的水流入乙中,乙每分钟水位上升![]() cm,1.5-
cm,1.5-![]() =
=![]() ,
,![]() 分,即开始注水后乙比甲高0.5cm的用时为
分,即开始注水后乙比甲高0.5cm的用时为![]() 分;
分;
当乙的水位达到5cm时开始流向甲,此时用时为![]() =
=![]() 分,甲水位每分上升
分,甲水位每分上升![]() cm,当甲的水位高为4.5cm时,乙比甲高0.5cm,此时用时
cm,当甲的水位高为4.5cm时,乙比甲高0.5cm,此时用时![]() =
=![]() 分;
分;
综上,开始注入![]() 分钟的水量后,甲与乙的水位高度之差是0.5cm
分钟的水量后,甲与乙的水位高度之差是0.5cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,
 ,点P按
,点P按 方向运动,到达点B时运动停止,运动开始时以每秒2个长度单位匀速运动,到达D点后,改为每秒m个单位匀速运动,到达C后,改为每秒n个单位匀速运动,在整个运动过程中,
方向运动,到达点B时运动停止,运动开始时以每秒2个长度单位匀速运动,到达D点后,改为每秒m个单位匀速运动,到达C后,改为每秒n个单位匀速运动,在整个运动过程中, 的面积S与运动时间t的函数关系如图所示.
的面积S与运动时间t的函数关系如图所示.
求:
 求AB、BC的长;
求AB、BC的长; 求m,n的值.
求m,n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以BC为底边的等腰
 ,点D,E,G分别在BC,AB,AC上,且
,点D,E,G分别在BC,AB,AC上,且 ,
, ,延长GE至点F,使得
,延长GE至点F,使得 .
. 求证:四边形BDEF为平行四边形;
求证:四边形BDEF为平行四边形; 当
当 ,
, 时,联结DF,求线段DF的长.
时,联结DF,求线段DF的长.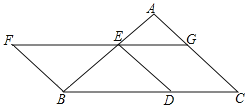
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+b与x轴交于点A、B,且A点的坐标为(1,0),与y轴交于点C(0,1).

(1)求抛物线的解析式,并求出点B坐标;
(2)过点B作BD∥CA交抛物线于点D,连接BC、CA、AD,求四边形ABCD的周长;(结果保留根号)
(3)在x轴上方的抛物线上是否存在点P,过点P作PE垂直于x轴,垂足为点E,使以B、P、E为顶点的三角形与△CBD相似?若存在请求出P点的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,点E是AD上的点,点F是BC的延长线上一点,CF=DE,连结BE和EF,EF与CD交于点G,且∠FBE=∠FEB.

(1)过点F作FH⊥BE于点H,证明: =
=  ;
;
(2)猜想:BE、AE、EF之间的数量关系,并证明你的结论;
(3)若DG=2,求AE值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,AB=6,EF=2,则BC长为( )

A.8
B.10
C.12
D.14 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( )

A.50°
B.51°
C.51.5°
D.52.5°
相关试题

