【题目】如图1,正方形ABCD的边长为6cm,点F从点B出发,沿射线AB方向以1cm/秒的速度移动,点E从点D出发,向点A以1cm/秒的速度移动(不到点A).设点E,F同时出发移动t秒.
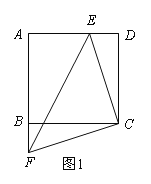

(1)在点E,F移动过程中,连接CE,CF,EF,则△CEF的形状是 ,始终保持不变;
(2)如图2,连接EF,设EF交BD于点M,当t=2时,求AM的长;
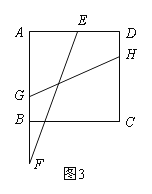
(3)如图3,点G,H分别在边AB,CD上,且GH=![]() cm,连接EF,当EF与GH的夹角为45°,求t的值.
cm,连接EF,当EF与GH的夹角为45°,求t的值.
参考答案:
【答案】(1)等腰直角三角形;(2)![]() ;(3)3.
;(3)3.
【解析】
试题(1)判断三角形CDE和三角形CBF全等是解题的关键;(2)此题过点E作EN∥AB,交BD于点N,证明△EMN≌△FMB,得出EM=FM,于是AM是直角三角形AEF斜边EF中线,只要求出EF长,AM长就求出来了;(3)设EF与GH交于P,连接CE,CF,若∠EPH=45°,前面已证∠EFC=45,显然GH∥CF,又有AF∥DC,可判断四边形GFCH是平行四边形,CF=GH=![]() ,在Rt△CBF中,用勾股定理求出BF长,即t值求出.
,在Rt△CBF中,用勾股定理求出BF长,即t值求出.
试题解析:(1)∵点E,F的运动速度相同,且同时出发移动t秒,∴DE=BF=t,又∵CD=CB,∠CDE=∠CBF,∴△CDE≌△CBF,∴CE=CF,∠DCE=∠BCF,∠ECF=∠ECB+∠BCF=∠ECB+∠DCE=90,∴△CEF的形状是等腰直角三角形;(2)先证△EMN≌△FMB,过点E作EN∥AB,交BD于点N,∴∠END=∠ABD=∠EDN=45°, ∴EN="ED=BF=2" ,可证△EMN≌△FMB(AAS),∴EM=FM,Rt△AEF中,AE=4,AF=6+2=8,EF=![]() ,∴AM=
,∴AM=![]() EF=
EF=![]() .(3)连接CE,CF,设EF与GH交于P,由(1)得∠CFE=45°,又∠EPH=45°,∴GH∥CF,又AF∥DC, ∴四边形GFCH是平行四边形 ,∴CF=GH=
.(3)连接CE,CF,设EF与GH交于P,由(1)得∠CFE=45°,又∠EPH=45°,∴GH∥CF,又AF∥DC, ∴四边形GFCH是平行四边形 ,∴CF=GH=![]() ,在Rt△CBF中,得BF=3,∴t=3.
,在Rt△CBF中,得BF=3,∴t=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,直线l1:
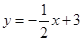 与x轴交于点A,与y轴交于点B,直线l2:
与x轴交于点A,与y轴交于点B,直线l2: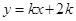 与x轴交于点C,与直线l1交于点P.
与x轴交于点C,与直线l1交于点P.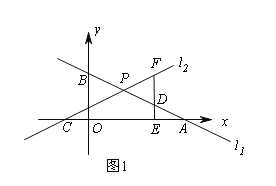
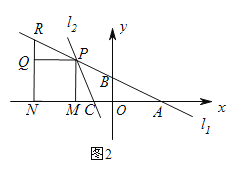
(1)当k=1时,求点P的坐标;
(2)如图1,点D为PA的中点,过点D作DE⊥x轴于E,交直线l2于点F,若DF=2DE,求k的值;
(3)如图2,点P在第二象限内,PM⊥x轴于M,以PM为边向左作正方形PMNQ,NQ的延长线交直线l1于点R,若PR=PC,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列一组图形中点的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,…,按此规律第6个图中共有点的个数是( )
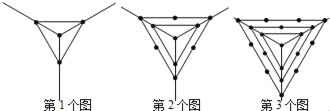
A.46B.63C.64D.73
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1:2:1,,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升
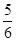 cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.
cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.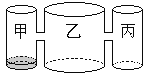
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,过点D作DE⊥AB于点E,作DF⊥BC于点F,连接EF.求证:(1)△ADE≌△CDF;(2)∠BEF=∠BFE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G.
(1)求证:△ACE≌△CBD;
(2)求∠CGE的度数.

相关试题

