【题目】探究:
(1)如图1,在△ABC中,∠A=40°,△ABC的内角平分线交于点P,求∠P的度数;
(2)如图2,在△ABC中,∠A=90°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB,连结PQ,求∠BQP的度数.

参考答案:
【答案】(1)110°;(2)60°
【解析】
(1)根据角平分线定理可知∠PBC+∠PCB =![]() ( ∠ABC+∠ACB ),∠A=40°已知,根据三角形内角和等于180°,可得∠ABC+∠ACB =140°,所以∠PBC+∠PCB =70°,再次根据三角形内角和可得∠P =110,即为答案.
( ∠ABC+∠ACB ),∠A=40°已知,根据三角形内角和等于180°,可得∠ABC+∠ACB =140°,所以∠PBC+∠PCB =70°,再次根据三角形内角和可得∠P =110,即为答案.
(2)根据BP、BQ三等分∠ABC,CP、CQ三等分∠ACB可得∠QBC+∠QCB=![]() ( ∠ABC+∠ACB )= 60°,所以∠BQC=120°,又由BP平分∠QBC, CP平分∠QCB,可得PQ平分∠BQC,所以∠BQP =
( ∠ABC+∠ACB )= 60°,所以∠BQC=120°,又由BP平分∠QBC, CP平分∠QCB,可得PQ平分∠BQC,所以∠BQP =![]() ×∠BQC =60° , 即得出答案.
×∠BQC =60° , 即得出答案.
解:(1)∵∠A+∠ABC+∠ACB = 180°
∴∠ABC+∠ACB=180° -∠A =140°
∵BP平分∠ABC, CP平分∠ACB
∴ ∠PBC+∠PCB=![]() ( ∠ABC+∠ACB )=70°
( ∠ABC+∠ACB )=70°
∵∠P+∠PBC+∠PCB = 180°
∴∠P=180°-(∠PBC+∠PCB)=110°
(2)∵∠A+∠ABC+ ∠ACB = 180°
∴∠ABC+∠ACB=180° -∠A =90°
∵BQ三等分∠ABC,CQ三等分∠ACB
∴ ∠QBC+∠QCB=![]() ( ∠ABC+∠ACB )=60°
( ∠ABC+∠ACB )=60°
∵∠Q+∠QBC+∠QCB= 180°
∴∠Q=180°-(∠QBC+∠QCB)=120°
∵BP平分∠QBC, CP平分∠QCB
∴PQ平分∠BQC
∴∠BQP =![]() ×120°=60°
×120°=60°
-
科目: 来源: 题型:
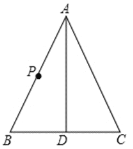
查看答案和解析>>【题目】如图,在△ABC中,AB=AC, AD是△ABC 底边BC上的中线,P为AB上一点.
(1)在AD上找一点E,使得PE+EB的值最小;
(2)若P为AB的中点,当∠BPE= °时,△ABC是等边三角形.(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;③线段BC是点B到AC的距离;⑥线段AC的长度是点A到BC的距离.

A.①④③⑥B.①④⑥C.②③D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字 ,
, ,
, ,
, ,如图
,如图 ,正方形
,正方形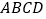 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图 起跳,第一次掷得
起跳,第一次掷得 ,就顺时针连续跳
,就顺时针连续跳 个边长,落到圈
个边长,落到圈 ;若第二次掷得
;若第二次掷得 ,就从
,就从 开始顺时针连续跳
开始顺时针连续跳 个边长,落到圈
个边长,落到圈 ;
; 设游戏者从圈
设游戏者从圈 起跳.
起跳.(
 )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈 的概率
的概率 .
.(
 )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈 的概率
的概率 ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈 的可能性一样吗?
的可能性一样吗?
-
科目: 来源: 题型:
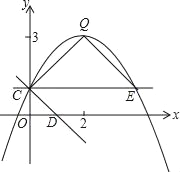
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点C(0,1),顶点为Q(2,3),点D在x轴正半轴上,且OD=OC.
(1)求直线CD的解析式;
(2)求抛物线的解析式;
(3)将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E,求证:△CEQ∽△CDO;
(4)在(3)的条件下,若点P是线段QE上的动点,点F是线段OD上的动点,问:在P点和F点移动过程中,△PCF的周长是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
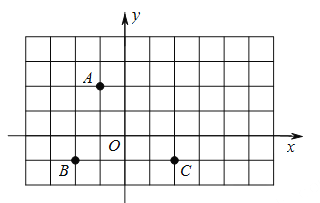
查看答案和解析>>【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,点A,B,C均在格点上.
(1)请值接写出点A,B,C的坐标.
(2)若平移线段AB,使B移动到C的位置,请在图中画出A移动后的位置D,依次连接B,C,D,A,并求出四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“数学运算”是数学学科核心素养之一,某校对七年级学生“数学运算能力”情况进行调研,从该校360名七年级学生中抽取了部分学生进行运算能力测试井进行分析,成绩分为A、B、C三个层次,绘制了频数分布表(如下),请根据图表信息解答下列问题:

(1)补全频数分布;
(2)如果成绩为A等级的同学属于优秀,请你估计该校七年级约有多少人达到优秀水平?
相关试题

