搜索
【题目】如图，∠ACB＝90°，CD⊥AB，垂足为D，则下面的结论中正确的是（ ）
①BC与AC互相垂直；②AC与CD互相垂直；③点A到BC的垂线段是线段BC；④点C到AB的垂线段是线段CD；③线段BC是点B到AC的距离；⑥线段AC的长度是点A到BC的距离．
A.①④③⑥B.①④⑥C.②③D.①④
参考答案：
【答案】B
【解析】
根据点到直线距离的定义对各选项进行逐一分析即可．
①BC与AC互相垂直；②AC与CD互相垂直；③点A到BC的垂线段是线段BC；④点C到AB的垂线段是线段CD；⑤线段BC是点B到AC的距离；⑥线段AC的长度是点A到BC的距离．
解：∵∠ACB＝90°，∴AC⊥BC，故①正确；
AC与DC相交不垂直，故②错误；
点A到BC的垂线段是线段AC，故③错误；
点C到AB的垂线段是线段CD，故④正确；
线段BC的长度是点B到AC的距离，故⑤错误；
线段AC的长度是点A到BC的距离，故⑥正确；
故选：B．
-
科目： 来源： 题型：
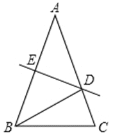
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC，DE垂直平分AB于E，交AC于D，连接BD．
（1）如果∠A＝40°，求∠CBD的度数；
（2）若AB＝AC＝9cm，BC＝5cm，求△BCD的周长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．
（1）求证：BE与⊙O相切；
（2）设OE交⊙O于点F，若DF=1，BC=2
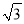，求阴影部分的面积．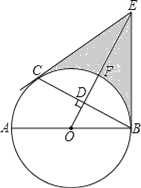
-
科目： 来源： 题型：
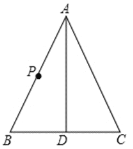
查看答案和解析>>【题目】如图，在△ABC中，AB＝AC， AD是△ABC 底边BC上的中线，P为AB上一点．
（1）在AD上找一点E，使得PE+EB的值最小；
（2）若P为AB的中点，当∠BPE＝ °时，△ABC是等边三角形．（直接写出结果）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图
，一枚质地均匀的正四面体骰子，它有四个面并分别标有数字，
，
，
，如图，正方形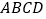
顶点处各有一个圈．跳圈游戏的规则为：游戏者每掷一次骰子，骰子着地一面上的数字是几，就沿正方形的边顺时针方向连续跳几个边长．如：若从图
起跳，第一次掷得，就顺时针连续跳个边长，落到圈
；若第二次掷得，就从开始顺时针连续跳个边长，落到圈
；
设游戏者从圈起跳．（
）嘉嘉随机掷一次骰子，求落回到圈的概率
．（
）淇淇随机掷两次骰子，用列表法求最后落回到圈的概率
，并指出她与嘉嘉落回到圈的可能性一样吗？
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：
（1）如图1，在△ABC中，∠A＝40°，△ABC的内角平分线交于点P，求∠P的度数；
（2）如图2，在△ABC中，∠A＝90°，BP、BQ三等分∠ABC，CP、CQ三等分∠ACB，连结PQ，求∠BQP的度数．
-
科目： 来源： 题型：
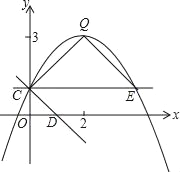
查看答案和解析>>【题目】如图，抛物线y=ax2+bx+c（a≠0）的图象过点C（0，1），顶点为Q（2，3），点D在x轴正半轴上，且OD=OC．
（1）求直线CD的解析式；
（2）求抛物线的解析式；
（3）将直线CD绕点C逆时针方向旋转45°所得直线与抛物线相交于另一点E，求证：△CEQ∽△CDO；
（4）在（3）的条件下，若点P是线段QE上的动点，点F是线段OD上的动点，问：在P点和F点移动过程中，△PCF的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．
相关试题
