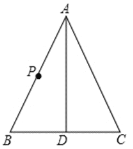
【题目】如图,在△ABC中,AB=AC, AD是△ABC 底边BC上的中线,P为AB上一点.
(1)在AD上找一点E,使得PE+EB的值最小;
(2)若P为AB的中点,当∠BPE= °时,△ABC是等边三角形.(直接写出结果)
参考答案:
【答案】(1)见解析;(2)90°
【解析】
(1)根据等腰三角形三线合一的性质可知AD垂直平分BC,再根据两点间距离最短的性质,连接CP交AD于点E,并连接BE,即可得到本题答案.
(2)因为P为AB的中点,要使△ABC是等边三角形,则需BC=AB,根据等腰三角形三线合一的性质,所以CP⊥AB,即∠BPE=90°.
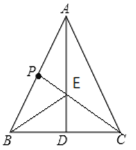
(1)如图,点E为所求.理由如下:
连接CP交AD于点E,并连接BE
∵AB=AC, AD是△ABC 底边BC上的中线
∴AD⊥BC,且BD=CD
∴BE=CE
∵两点间线段最短
∴PE+EB=PC
∴下图中E点即为所求.
(2)90°.理由如下:
∵△ABC是等边三角形
∴BC=AB
∵P为AB的中点
∴BP=AP
∴CP⊥AB
∴∠BPE=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.如图,点A、B、D、E在⊙O上,弦AE、BD的延长线相交于点C.若AB是⊙O的直径,D是BC的中点.
(1)试判断AB、AC之间的大小关系,并给出证明;
(2)在上述题设条件下,当△ABC为正三角形时,点E是否AC的中点?为什么?

-
科目: 来源: 题型:
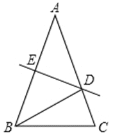
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE垂直平分AB于E,交AC于D,连接BD.
(1)如果∠A=40°,求∠CBD的度数;
(2)若AB=AC=9cm,BC=5cm,求△BCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2
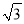 ,求阴影部分的面积.
,求阴影部分的面积.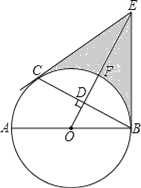
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB=90°,CD⊥AB,垂足为D,则下面的结论中正确的是( )
①BC与AC互相垂直;②AC与CD互相垂直;③点A到BC的垂线段是线段BC;④点C到AB的垂线段是线段CD;③线段BC是点B到AC的距离;⑥线段AC的长度是点A到BC的距离.

A.①④③⑥B.①④⑥C.②③D.①④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字 ,
, ,
, ,
, ,如图
,如图 ,正方形
,正方形 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图 起跳,第一次掷得
起跳,第一次掷得 ,就顺时针连续跳
,就顺时针连续跳 个边长,落到圈
个边长,落到圈 ;若第二次掷得
;若第二次掷得 ,就从
,就从 开始顺时针连续跳
开始顺时针连续跳 个边长,落到圈
个边长,落到圈 ;
; 设游戏者从圈
设游戏者从圈 起跳.
起跳.(
 )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈 的概率
的概率 .
.(
 )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈 的概率
的概率 ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈 的可能性一样吗?
的可能性一样吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:
(1)如图1,在△ABC中,∠A=40°,△ABC的内角平分线交于点P,求∠P的度数;
(2)如图2,在△ABC中,∠A=90°,BP、BQ三等分∠ABC,CP、CQ三等分∠ACB,连结PQ,求∠BQP的度数.

相关试题

