【题目】等边![]() 边长为
边长为![]() ,
,![]() 为
为![]() 边上一点,
边上一点,![]() ,且
,且![]() 、
、![]() 分别于边
分别于边![]() 、
、![]() 交于点
交于点![]() 、
、![]() .
.
![]() 如图
如图![]() ,当点
,当点![]() 为
为![]() 的三等分点,且
的三等分点,且![]() 时,判断
时,判断![]() 的形状;
的形状;
![]() 如图
如图![]() ,若点
,若点![]() 在
在![]() 边上运动,且保持
边上运动,且保持![]() ,设
,设![]() ,四边形
,四边形![]() 面积的
面积的![]() ,求
,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 如图
如图![]() ,若点
,若点![]() 在
在![]() 边上运动,且
边上运动,且![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 时,求
时,求![]() 的长.
的长.

参考答案:
【答案】(1)详见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)根据三等分点的定义,求得BP与PC的长,进而根据直角三角形中30度的锐角所对的直角边等于斜边的一半,即可求得BE的长,即可作出判断;
(2)分别表示出△ABC、△BPE、△PCF的面积,根据四边形AEPF的面积=△ABC的面积-△BPE的面积-△PCF的面积,即可求解;
(3)首先证明△BPE∽△CFP,根据相似三角形的对应边的比相等即可求得BP的长,进而即可求得PE的长.
![]() ∵点
∵点![]() 为
为![]() 的三等分点,
的三等分点,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴在直角![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 是等边三角形;
是等边三角形;
![]() 的面积是:
的面积是:![]() ;
;
![]() ,则
,则![]() .
.![]() ,
,![]() ,
,![]() .
.
则![]() 的面积是:
的面积是:![]() ,
,
![]() 的面积是:
的面积是:![]() .
.
∴四边形![]() 面积的
面积的![]() ;
;
即![]() ;
;
![]() ∵在
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,则
,则![]() .
.
∴![]() ,
,
解得:![]() 或
或![]() .
.
当![]() 时,在三角形
时,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
则![]() ;
;
当![]() 时,在三角形
时,在三角形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
则![]() 是等边三角形,∴
是等边三角形,∴![]() .
.
故![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在探究三角形的内角和的小组活动中,小颖作如下辅助线:延长△ABC的边BC到D,作CE∥AB,于是小颖得出三角形内角和的证明方法.
(1)求证:∠A+∠B+∠ACB=180°;
(2)如果CE平分∠ACD,AC=5,求BC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC是△ABD的角平分线,BC=DC,∠A=∠E=30°,∠D=50°.
(1)写出AB=DE的理由;
(2)求∠BCE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 和
和 中,
中, ,
,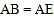 ,
,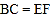 ,
, ,
, ;
;
 请说明
请说明 的理由;
的理由; 可以经过图形的变换得到
可以经过图形的变换得到 ,请你描述这个变换;
,请你描述这个变换; 求
求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,在边长为
,在边长为 的小正方形组成的网格中,
的小正方形组成的网格中, 的顶点
的顶点 、
、 均在格点上,点
均在格点上,点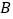 在
在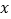 轴上,点
轴上,点 的坐标为
的坐标为 .
.
 点
点 关于点
关于点 中心对称的点的坐标为________;
中心对称的点的坐标为________; 绕点
绕点 顺时针旋转
顺时针旋转 后得到
后得到 ,那么点
,那么点 的坐标为________;线段
的坐标为________;线段 在旋转过程中所扫过的面积是________.
在旋转过程中所扫过的面积是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,AE⊥BD于E,若∠OAE=24°,则∠BAE的度数是( )

A. 24° B. 33° C. 42° D. 43°
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的例题:
解方程

解:(1)当x≥0时,
原方程化为x2 – x –2=0,
解得:x1=2,x2= - 1(不合题意,舍去)
(2)当x<0时,
原方程化为x2 + x –2=0,
解得:x1=1,(不合题意,舍去)x2= -2
∴原方程的根是x1=2, x2= - 2
(3)请参照例题解方程

相关试题

