【题目】如图,在探究三角形的内角和的小组活动中,小颖作如下辅助线:延长△ABC的边BC到D,作CE∥AB,于是小颖得出三角形内角和的证明方法.
(1)求证:∠A+∠B+∠ACB=180°;
(2)如果CE平分∠ACD,AC=5,求BC的长.

参考答案:
【答案】(1)证明见解析(2)5
【解析】
(1)根据两直线平行,同位角相等可得∠B=∠1,两直线平行,内错角相等可得∠A=∠2,再根据平角的定义列式整理即可得证.
(2)根据CE平分∠ACD,即可得出∠1=∠2,再根据平行线的性质,即可得到∠A=∠B,即可得到AC=BC.
(1)如图,延长BC到D,过点C作CE∥BA,
∵BA∥CE,
∴∠A=∠1(两直线平行,内错角相等),
∠B=∠2(两直线平行,同位角相等),
又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),
∴∠A+∠B+∠ACB=180°(等量代换).
(2)∵CE平分∠ACD,
∴∠1=∠2,
又∵CE∥AB,
∴∠1=∠A,∠2=∠B,
∴∠A=∠B,
∴AC=BC=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】节能环保的油电混合动力汽车,既可用油做动力行驶,也可用电做动力行驶,某品牌油电混合动力汽车从甲地行驶到乙地,若完全用油做动力行驶,则费用为80元;若完全用电做动力行驶,则费用为30元,已知汽车行驶中每千米用油费用比用电费用多0.5元.
(1)求汽车行驶中每千米用电费用是多少元?
(2)甲、乙两地的距离是多少千米?
-
科目: 来源: 题型:
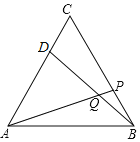
查看答案和解析>>【题目】如图,在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发,分别都以每分钟1个单位的速度由C向A和由B向C爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?
(2)在爬行过程中BD与AP所成的∠DQA有变化吗?若无变化是多少度?
-
科目: 来源: 题型:
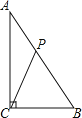
查看答案和解析>>【题目】如图,在△ABC中,已知∠ACB=90°,AB=10cm,AC=8cm,动点P从点A出发,以2cm/s的速度沿线段AB向点B运动,在运动过程中,当△APC为等腰三角形时,点P出发的时间t可能的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BC是△ABD的角平分线,BC=DC,∠A=∠E=30°,∠D=50°.
(1)写出AB=DE的理由;
(2)求∠BCE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 和
和 中,
中, ,
,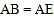 ,
,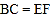 ,
, ,
, ;
;
 请说明
请说明 的理由;
的理由; 可以经过图形的变换得到
可以经过图形的变换得到 ,请你描述这个变换;
,请你描述这个变换; 求
求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】等边
 边长为
边长为 ,
, 为
为 边上一点,
边上一点,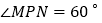 ,且
,且 、
、 分别于边
分别于边 、
、 交于点
交于点 、
、 .
. 如图
如图 ,当点
,当点 为
为 的三等分点,且
的三等分点,且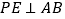 时,判断
时,判断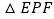 的形状;
的形状; 如图
如图 ,若点
,若点 在
在 边上运动,且保持
边上运动,且保持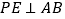 ,设
,设 ,四边形
,四边形 面积的
面积的 ,求
,求 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围; 如图
如图 ,若点
,若点 在
在 边上运动,且
边上运动,且 绕点
绕点 旋转,当
旋转,当 时,求
时,求 的长.
的长.
相关试题

